题目内容
已知函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,若数列{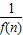 }的前n项和为Sn,则S2010的值 .
}的前n项和为Sn,则S2010的值 .
【答案】分析:先利用函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,求出a;代入即可求出数列{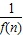 }的通项公式,再利用错位相减法求和法即可求出S2010的值.
}的通项公式,再利用错位相减法求和法即可求出S2010的值.
解答:解:∵f(x)=ax2-1,∴f′(x)=2ax,
所以f′(1)=2a=8,得a=4.
所以f(x)=4x2-1,
故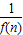 =
=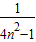 =
= (
(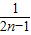 -
-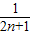 )
)
∴S2010= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(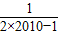 -
-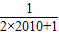 )]
)]
= (1-
(1-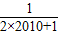 )=
)=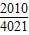 .
.
故答案为: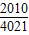 .
.
点评:本题主要是对函数知识和数列知识的综合考查.解决本题的关键是利用函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,求出a的值以及错位相减法的应用
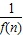 }的通项公式,再利用错位相减法求和法即可求出S2010的值.
}的通项公式,再利用错位相减法求和法即可求出S2010的值.解答:解:∵f(x)=ax2-1,∴f′(x)=2ax,
所以f′(1)=2a=8,得a=4.
所以f(x)=4x2-1,
故
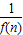 =
=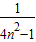 =
= (
(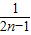 -
-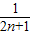 )
)∴S2010=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(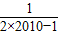 -
-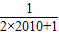 )]
)]=
 (1-
(1-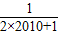 )=
)=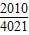 .
.故答案为:
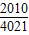 .
.点评:本题主要是对函数知识和数列知识的综合考查.解决本题的关键是利用函数f(x)=ax2-1的图象在点A(1,f(1))处的切线l与直线8x-y+2=0平行,求出a的值以及错位相减法的应用

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目