题目内容
设PMN是⊙O通过圆心的一条割线，PAB是另一条割线，M、N、A、B是这两条割线与圆的交点，求证：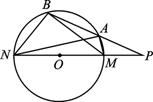
是一个定值.
证明：因A、B、M、N四点共圆，则∠ANM=∠ABM，△PAN∽△PMB，于是
= .又∠PAM=∠PNB，∠P为公共角，则△PAM∽△PNB，
.
因而，
，又P是定点，PM=a为定值，设圆的半径为R，则
=
（定值）.
练习册系列答案
阅读快车系列答案
相关题目
是一个定值.阅读快车系列答案题目内容
设PMN是⊙O通过圆心的一条割线，PAB是另一条割线，M、N、A、B是这两条割线与圆的交点，求证：是一个定值.
证明：因A、B、M、N四点共圆，则∠ANM=∠ABM，△PAN∽△PMB，于是= .又∠PAM=∠PNB，∠P为公共角，则△PAM∽△PNB，.
因而，，又P是定点，PM=a为定值，设圆的半径为R，则=（定值）.
阅读快车系列答案