题目内容
若 ,
, 在区间
在区间 上是增函数,则方程
上是增函数,则方程 有且只有一解时p的取值范围是 .
有且只有一解时p的取值范围是 .
【答案】分析:由题意可得: =3x2+(p+2)x+3,结合题中条件可得:f(x)在[0,+∞)单调递增,原方程等价于方程
=3x2+(p+2)x+3,结合题中条件可得:f(x)在[0,+∞)单调递增,原方程等价于方程 在[0,+∞)上只有一解,由f(x)≥3,所以
在[0,+∞)上只有一解,由f(x)≥3,所以 ≥3在[0,+∞)上有解,进而求出p的数值.
≥3在[0,+∞)上有解,进而求出p的数值.
解答:解:∵ ,
,
∴ =3x2+(p+2)x+3,并且其对称轴为:x=-
=3x2+(p+2)x+3,并且其对称轴为:x=- ,
,
∵f(x)在区间 上是增函数,
上是增函数,
∴f(x)在[0,+∞)单调递增,
∵方程 有且只有一解
有且只有一解
∴方程 在[0,+∞)上只有一解,
在[0,+∞)上只有一解,
∵f(x)≥3,
∴ ≥3在[0,+∞)上有解,
≥3在[0,+∞)上有解,
∴p≥3.
故答案为:p≥3.
点评:本题主要考查二次函数的性质与幂函数的值域问题,以及考查方程的有解的知识点,此题综合性较强属于中档题,考查学生的分析问题解决问题的能力.
 =3x2+(p+2)x+3,结合题中条件可得:f(x)在[0,+∞)单调递增,原方程等价于方程
=3x2+(p+2)x+3,结合题中条件可得:f(x)在[0,+∞)单调递增,原方程等价于方程 在[0,+∞)上只有一解,由f(x)≥3,所以
在[0,+∞)上只有一解,由f(x)≥3,所以 ≥3在[0,+∞)上有解,进而求出p的数值.
≥3在[0,+∞)上有解,进而求出p的数值.解答:解:∵
 ,
,∴
 =3x2+(p+2)x+3,并且其对称轴为:x=-
=3x2+(p+2)x+3,并且其对称轴为:x=- ,
,∵f(x)在区间
 上是增函数,
上是增函数,∴f(x)在[0,+∞)单调递增,
∵方程
 有且只有一解
有且只有一解∴方程
 在[0,+∞)上只有一解,
在[0,+∞)上只有一解,∵f(x)≥3,
∴
 ≥3在[0,+∞)上有解,
≥3在[0,+∞)上有解,∴p≥3.
故答案为:p≥3.
点评:本题主要考查二次函数的性质与幂函数的值域问题,以及考查方程的有解的知识点,此题综合性较强属于中档题,考查学生的分析问题解决问题的能力.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ,
, 在区间
在区间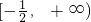 上是增函数,则方程
上是增函数,则方程 有且只有一解时p的取值范围是________.
有且只有一解时p的取值范围是________.