题目内容
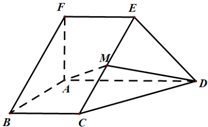 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=| 1 | 2 |
(I)求异面直线BF与DE所成的角的大小;
(II)证明平面AMD⊥平面CDE.
分析:(1)如图所示,分别以AB、AD、AF为x轴、y轴、z轴,建立空间直角坐标系.算出B、C、D、E、F、M各点的坐标,从而得到
、
的坐标,利用空间向量的夹角公式算出cos<
,
>的值,即得异面直线BF与DE所成的角的大小;
(2)利用数量积为零的两个向量相互垂直,证出AM⊥CE且DM⊥CE,从而证出CE⊥平面AMD,结合面面垂直判定定理,即可证出平面AMD⊥平面CDE.
| BF |
| DE |
| BF |
| DE |
(2)利用数量积为零的两个向量相互垂直,证出AM⊥CE且DM⊥CE,从而证出CE⊥平面AMD,结合面面垂直判定定理,即可证出平面AMD⊥平面CDE.
解答:解:分别以AB、AD、AF为x轴、y轴、z轴,建立空间直角坐标系,如图所示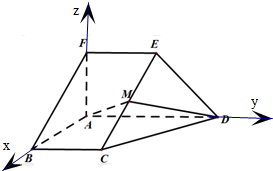
设AB=1,依题意得B(1,0,0),C(1,1,0),D(0,2,0)
E(0,1,1),F(0,0,1),M(
,1,
)
( I)
=(-1,0,1),
=(0,-1,1)
∴
•
=-1×0+0×(-1)+1×1=1
|
|=
=
,|
|=
=
可得cos<
,
>=
=
=
∵<
,
>的范围是[0,π],∴<
,
>=
所以异面直线BF与DE所成的角的大小为
.
( II)∵
=(
,1,
),
=(-1,0,1),
∴
•
=
×(-1)+1×0+
×1=0,得
⊥
,
同理可得:
•
=0,得
⊥
∵AM、DM是平面AMD内的相交直线,∴CE⊥平面AMD
又∵CE?平面CDE,∴平面AMD⊥平面CDE.

设AB=1,依题意得B(1,0,0),C(1,1,0),D(0,2,0)
E(0,1,1),F(0,0,1),M(
| 1 |
| 2 |
| 1 |
| 2 |
( I)
| BF |
| DE |
∴
| BF |
| DE |
|
| BF |
| (-1)2+02+12 |
| 2 |
| DE |
| 02+(-1)2+12 |
| 2 |
可得cos<
| BF |
| DE |
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∵<
| BF |
| DE |
| BF |
| DE |
| π |
| 3 |
所以异面直线BF与DE所成的角的大小为
| π |
| 3 |
( II)∵
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| CE |
∴
| AM |
| CE |
| 1 |
| 2 |
| 1 |
| 2 |
| AM |
| CE |
同理可得:
| DM |
| CE |
| DM |
| CE |
∵AM、DM是平面AMD内的相交直线,∴CE⊥平面AMD
又∵CE?平面CDE,∴平面AMD⊥平面CDE.
点评:本题给出特殊五面体,求证面面垂直并求线线所成的角,着重考查了利用空间坐标系解决异面直线所成角和证明面面垂直等知识点,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
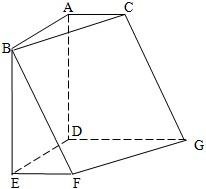 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=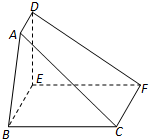 如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE.
如图,在五面体ABC-DEF中,四边形BCFE 是矩形,DE⊥平面BCFE. ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.