题目内容
试讨论函数f(x)=x+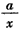 (a≠0)在(0,+∞)上的单调性。
(a≠0)在(0,+∞)上的单调性。
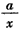 (a≠0)在(0,+∞)上的单调性。
(a≠0)在(0,+∞)上的单调性。解:任取x1,x2∈(0,+∞)且x1<x2,
则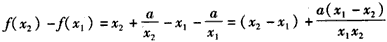
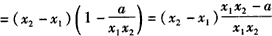 ,
,
若a<0,则由x2-x1>0,x1x2>0,x1x2-a>0知f(x2)-f(x1)>0,即f(x2)>f(x1),
由单调性定义可知,f(x)在(0,+∞)上单调递增;
若a>0,
则当0<x1<x2≤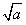 时,会有x2-x1>0,x1x2>0,x1x2-a<0,因此f(x2)-f(x1)<0,即f(x2)<f(x1);
时,会有x2-x1>0,x1x2>0,x1x2-a<0,因此f(x2)-f(x1)<0,即f(x2)<f(x1);
当x2>x1>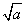 时,会有x2-x1>0,x1x2>0,x1x2-a>0,因此f(x2)-f(x1)>0,即f(x2)>f(x1),
时,会有x2-x1>0,x1x2>0,x1x2-a>0,因此f(x2)-f(x1)>0,即f(x2)>f(x1),
由单调性定义可知f(x)在(0,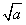 ]上单调递减,在[
]上单调递减,在[ ,+∞)上单调递增;
,+∞)上单调递增;
综上可知,当a<0时,f(x)=x+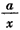 在(0,+∞)上单调递增;
在(0,+∞)上单调递增;
当a>0时f(x)=x+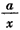 在(0,
在(0,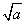 ]上单调递减,在[
]上单调递减,在[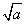 ,+∞)上单调递增。
,+∞)上单调递增。
则
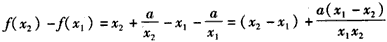
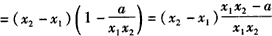 ,
,若a<0,则由x2-x1>0,x1x2>0,x1x2-a>0知f(x2)-f(x1)>0,即f(x2)>f(x1),
由单调性定义可知,f(x)在(0,+∞)上单调递增;
若a>0,
则当0<x1<x2≤
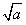 时,会有x2-x1>0,x1x2>0,x1x2-a<0,因此f(x2)-f(x1)<0,即f(x2)<f(x1);
时,会有x2-x1>0,x1x2>0,x1x2-a<0,因此f(x2)-f(x1)<0,即f(x2)<f(x1); 当x2>x1>
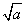 时,会有x2-x1>0,x1x2>0,x1x2-a>0,因此f(x2)-f(x1)>0,即f(x2)>f(x1),
时,会有x2-x1>0,x1x2>0,x1x2-a>0,因此f(x2)-f(x1)>0,即f(x2)>f(x1),由单调性定义可知f(x)在(0,
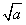 ]上单调递减,在[
]上单调递减,在[ ,+∞)上单调递增;
,+∞)上单调递增;综上可知,当a<0时,f(x)=x+
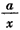 在(0,+∞)上单调递增;
在(0,+∞)上单调递增;当a>0时f(x)=x+
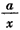 在(0,
在(0,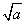 ]上单调递减,在[
]上单调递减,在[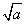 ,+∞)上单调递增。
,+∞)上单调递增。 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
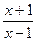 (a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
(a>0且a≠1)在(1,+∞)上的单调性,并予以证明.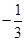 ax
3 + x2 + 2 ( a ≠ 0 ) .
ax
3 + x2 + 2 ( a ≠ 0 ) .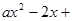 1 .
1 .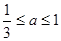 ,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),
,且f(x)在区间[1,3]上的最大值为M(a) ,最小值为N(a),