题目内容

等差数列{an}的前n项和为Sn,已知S10=0,S15=25,则nSn的最小值为　　　　.

【解析】由题意知: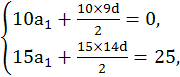解得d=,

a1=-3,所以Sn=-3n+×=,

即nSn=,令f(n)=,

则有f′(n)=n2-,令f′(n)>0,得n>,

令f′(n)<0,得0<n<.又因为n为正整数,所以当n=7时,f(n)=取得最小值,即nSn的最小值为-49.

答案:-49

练习册系列答案
相关题目
设等差数列{an}的前n项和为Sn，若-a7＜a1＜-a8，则必定有（　　）
已知等差数列{an}的前n项和为Sn，且满足a2=6，S5=50，数列{bn}的前n项和Tn满足Tn+
1
2
bn=1．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证：数列{bn}为等比数列；
（Ⅲ）记cn=
1
4
an•bn，数列{cn}的前n项和为Rn，若Rn＜λ对n∈N*恒成立，求λ的最小值．
已知等差数列{an}的前2006项的和S2006=2008，其中所有的偶数项的和是2，则a1003的值为
2
2
．
等差数列{an}的前n项和为Sn，a1=1；等比数列{bn}中，b1=1．若a3+S3=14，b2S2=12
（Ⅰ）求an与bn；
（Ⅱ）设cn=an+2bn(n∈N*)，数列{cn}的前n项和为Tn．若对一切n∈N*不等式Tn≥λ恒成立，求λ的最大值．
设等差数列{an}的前n项和为Sn，则a5+a6＞0是S8≥S2的（　　）
A、充分而不必要条件B、必要而不充分条件C、充分必要条件D、既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网