题目内容
11.已知椭圆C的两个焦点分别为F1(0,-2$\sqrt{2}$),F2(0,2$\sqrt{2}$),离心率e=$\frac{2\sqrt{2}}{3}$.(1)求椭圆C的方程.
(2)一条斜率为-9的直线l与椭圆C交于不同的两点M,N,求线段MN的中点横坐标x0的取值范围.
(3)若椭圆C上存在不同两点关于直线y=$\frac{1}{9}$x+m对称,试求m的取值范围.
分析 (1)利用椭圆c=2$\sqrt{2}$,e=$\frac{2\sqrt{2}}{3}$,求出a,b,即可得出椭圆的方程;
(2)利用点差法,直线l的斜率,可得MN的中点坐标,利用MN的中点在椭圆$\frac{{y}^{2}}{9}+{x}^{2}=1$内,从而可得线段MN的中点横坐标x0的取值范围.
(3)若椭圆C上存在不同两点关于直线y=$\frac{1}{9}$x+m对称,由(2)知,线段MN的中点在直线y=$\frac{1}{9}$x+m,即可求m的取值范围.
解答 解:(1)设椭圆方程为$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}=1$,
由已知c=2$\sqrt{2}$,e=$\frac{2\sqrt{2}}{3}$.
解得a=3,b=1,
∴椭圆方程为:$\frac{{y}^{2}}{9}+{x}^{2}=1$;
(2)设M(x1,y2),N(x2,y2),MN的中点为P(x0,t),
由中点坐标公式有:x1+x2=2x0,y1+y2=2t,
M(x1,y2),N(x2,y2),代入椭圆方程相减可得kAB=-$\frac{9{x}_{0}}{t}$=-9
解得t=x0,
∵MN的中点为P(x0,t)在椭圆$\frac{{y}^{2}}{9}+{x}^{2}=1$内,
∴$\frac{{{x}_{0}}^{2}}{9}+{{x}_{0}}^{2}<1$,
∴-$\frac{\sqrt{10}}{10}$<x0<$\frac{\sqrt{10}}{10}$;
(3)若椭圆C上存在不同两点关于直线y=$\frac{1}{9}$x+m对称,由(2)知,线段MN的中点在直线y=$\frac{1}{9}$x+m,
∴x0=$\frac{1}{9}$x0+m,
∴m=$\frac{8}{9}$x0,
∵-$\frac{\sqrt{10}}{10}$<x0<$\frac{\sqrt{10}}{10}$;
∴-$\frac{4\sqrt{10}}{45}$<m<$\frac{4\sqrt{10}}{45}$.
点评 本题考查椭圆的方程,考查直线与椭圆的位置关系,考查点差法的运用,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | x+2y+8=0 | B. | x+2y-8=0 | C. | x-2y-8=0 | D. | x-2y+8=0 |
| A. | 用平行于圆锥底面的平面截圆锥,截面和底面之间的部分是圆台 | |
| B. | 以直角梯形的一腰为旋转轴,另一腰为母线的旋转面是圆台的侧面 | |
| C. | 圆锥、圆柱、圆台的底面都是圆 | |
| D. | 圆台的母线延长后与轴交于同一点 |
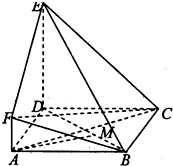 如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.
如图,ABCD是边长为3的正方形,AF∥DE,DE=3AF.