Question

2．已知过原点O的直线与函数y=log₉x的图象交于A，B两点，分别过A，B作y轴的平行线与函数y=log₃x的图象 交于C，D两点，当BC∥x轴时，A点的横坐标是（　　）

• A． $\sqrt{2}$
• B． 2
• C． $\sqrt{3}$
• D． 3

Answer 1

分析 可分别设A（x₁，log₉x₁），B（x₂，log₉x₂），A，B在过点O的直线上，从而便有$\frac{lo{g}_{9}{x}_{1}}{{x}_{1}}=\frac{lo{g}_{9}{x}_{2}}{{x}_{2}}$（1），可得到点C的纵坐标为log₃x₁，根据BC∥x轴便可得到log₃x₁=log₉x₂，从而可得到${x}_{2}={{x}_{1}}^{2}$，带入（1）式便可求出x₁，即求出C点的横坐标．

解答 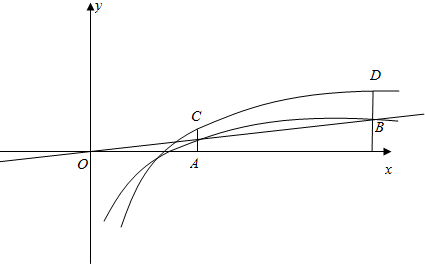解：如图，设点A，B的横坐标分别为x₁，x₂，由题设知，x₁＞1，x₂＞1；
∴A，B点的纵坐标分别为log₉x₁，log₉x₂；
∵A，B在过点O的直线上；
∴$\frac{lo{g}_{9}{x}_{1}}{{x}_{1}}=\frac{lo{g}_{9}{x}_{2}}{{x}_{2}}$；
点C，D的坐标分别为（x₁，log₃x₁），（x₂，log₃x₂）；
∵BC∥x轴；
∴log₃x₁=log₉x₂；
∴$lo{g}_{3}{x}_{1}=\frac{lo{g}_{3}{x}_{2}}{2}$；
∴${x}_{2}={{x}_{1}}^{2}$；
∴$\frac{lo{g}_{9}{x}_{1}}{{x}_{1}}=\frac{lo{g}_{9}{{x}_{1}}^{2}}{{{x}_{1}}^{2}}$；
∴x₁=2．
故选B．

点评 考查根据点的坐标求直线的斜率，以及对数的运算性质，对数函数的单调性．