题目内容
变量x,y满足约束条件
则目标函数z=3|x|+|y-3|的取值范围是( )
|
分析:确定不等式表示的区域,化简目标函数,利用图象即可求得结论.
解答: 解:不等式表示的区域如图所示,三个交点坐标分别为(0,1),(
解:不等式表示的区域如图所示,三个交点坐标分别为(0,1),(
,3),(2,0)
目标函数z=3|x|+|y-3|=3x-y+3,即y=-3x+z-3,
∴目标函数过(2,0)时,取得最大值为9,过(
,3)时,取得最小值为
∴目标函数z=3|x|+|y-3|的取值范围是[
,9]
故选A.
 解:不等式表示的区域如图所示,三个交点坐标分别为(0,1),(
解:不等式表示的区域如图所示,三个交点坐标分别为(0,1),(| 1 |
| 2 |
目标函数z=3|x|+|y-3|=3x-y+3,即y=-3x+z-3,
∴目标函数过(2,0)时,取得最大值为9,过(
| 1 |
| 2 |
| 3 |
| 2 |
∴目标函数z=3|x|+|y-3|的取值范围是[
| 3 |
| 2 |
故选A.
点评:本题考查线性规划知识的运用,考查数形结合的数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 ,则z=2x+y的最小值是
,则z=2x+y的最小值是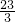

 ,则z=2x+y的最小值是( )
,则z=2x+y的最小值是( )

 ,则z=2x+y的最小值是( )
,则z=2x+y的最小值是( )

 ,且
,且 ,若变量x,y满足约束条
,若变量x,y满足约束条 ,则z的最大值为
,则z的最大值为