题目内容
15.若a>0,b>0,a+b=2,则2a+2b的最小值为4.分析 由于a>0,b>0,a+b=2,运用基本不等式和指数的运算性质,即可得到最小值.
解答 解:由于a>0,b>0,a+b=2,
则2a+2b≥2$\sqrt{{2}^{a}•{2}^{b}}$=2$\sqrt{{2}^{a+b}}$=2$\sqrt{4}$=4.
当且仅当a=b=1,取得最小值4.
故答案为:4.
点评 本题考查基本不等式的运用:求最值,同时考查指数的运算性质,考查运算能力,属于基础题.

练习册系列答案
相关题目
20.已知幂函数y=xn,y=xm,y=xp的图象如图,则( )
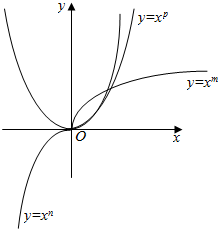

| A. | m>n>p | B. | m>p>n | C. | n>p>m | D. | p>n>m |