题目内容
20.某三棱锥的三视图如图所示,则该三棱锥的四个面中,面积最大的面的面积是$\sqrt{7}$
分析 由三视图想象出直观图,一般需从俯视图构建直观图,先确定最大的面,再求其面积.
解答 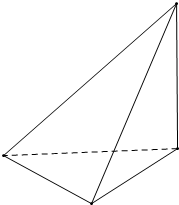 解:由三视图可知,该几何体有两个面是直角三角形,如右图,
解:由三视图可知,该几何体有两个面是直角三角形,如右图,
底面是正三角形,
最大的面是第四个面,
其边长分别为:
2,$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$;
故其面积为:
$\frac{1}{2}$×2×$\sqrt{8-1}$=$\sqrt{7}$;
故答案为:$\sqrt{7}$.
点评 三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目