题目内容
设函数 的图像关于直线
的图像关于直线 对称,它的周期是
对称,它的周期是 ,则( )
,则( )
A. 的图象过点 的图象过点 |
B. 在 在 上是减函数 上是减函数 |
C. 的一个对称中心是 的一个对称中心是 |
D.将 的图象向右平移 的图象向右平移 个单位得到函数 个单位得到函数 的图象 的图象 |
C
解析试题分析:根据题意,由于函数 的图像关于直线
的图像关于直线 对称,可知
对称,可知 它的周期是
它的周期是 ,可知w=2,
,可知w=2, ,那么可知
,那么可知 ,那么可知解析式,当x=0代入可知函数值不是为
,那么可知解析式,当x=0代入可知函数值不是为 A错误,对于B,由于将
A错误,对于B,由于将 代入解析式判定函数不具有单调性,故错误。对于D,由于将
代入解析式判定函数不具有单调性,故错误。对于D,由于将 的图象向右平移
的图象向右平移 个单位得到函数
个单位得到函数 的图象,g故错误,因此选C.
的图象,g故错误,因此选C.
考点:三角函数的性质
点评:解决的关键是对于对称性的理解以及图像变换的准确表示,属于基础题。

练习册系列答案
相关题目
函数 在一个周期内的图象如下,此函数的解析式为( )
在一个周期内的图象如下,此函数的解析式为( )
A. | B. |
C. | D. |
 的值域是( )
的值域是( )
A. | B. | C. | D. |
定义在 上的偶函数
上的偶函数 满足
满足 若
若 时解析为
时解析为 ,则
,则 >0的解集是
>0的解集是
A. | B. |
C. | D. |
若点P(sinα-cosα,tanα)在第一象限,则在[0,2p)内α的取值范围是 ( )
A.( , ,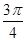 )∪(p, )∪(p,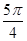 ) ) | B.( , , )∪(p, )∪(p,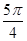 ) ) |
C.( , ,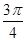 )∪( )∪(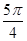 , ,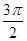 ) ) | D.( , ,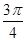 )∪( )∪(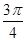 ,p) ,p) |
将函数 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函数解析式是( )
个单位, 再向上平移1个单位,所得图象的函数解析式是( )
A. +1 +1 | B. | C. | D. |
如图所示,是函数y=Asin(ωx+φ)(A>0,ω>0, -p<φ<0)的简图,则振幅、周期、初相分别是 ( )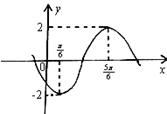
A.2, ,? ,? | B.2, ,? ,?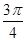 |
C.4, ,? ,?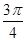 | D.2,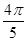 ,? ,? |
函数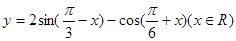 的最小值是( )
的最小值是( )
A. | B.-2 | C.-1 | D.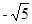 |
为了得到函数 的图象,只需将函数
的图象,只需将函数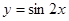 的图
的图
象( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |