题目内容
设向量 与
与 的夹角为120°,且满足|
的夹角为120°,且满足| |=|
|=| |=1,则|
|=1,则| +t
+t |(t∈R)的最小值是________.
|(t∈R)的最小值是________.

分析:由题意,可先求|
 +t
+t |2(t∈R)的最小值,将|
|2(t∈R)的最小值,将| +t
+t |2展开,代入题设条件,
|2展开,代入题设条件, ,
, 两向量的夹角为120°,模都是1,则可得|
两向量的夹角为120°,模都是1,则可得| +t
+t |2=t2-t+1,由于t∈R,求此二次函数的最小值即可得到|
|2=t2-t+1,由于t∈R,求此二次函数的最小值即可得到| +t
+t |2(t∈R)的最小值,再求其算术平方根,即可得到|
|2(t∈R)的最小值,再求其算术平方根,即可得到| +t
+t |的最小值,得到正确答案
|的最小值,得到正确答案解答:由题意,可先求|
 +t
+t |2(t∈R)的最小值
|2(t∈R)的最小值由于|
 +t
+t |2=
|2= +
+ +2t
+2t •
•
又由题意,
 ,
, 两向量的夹角为120°,模都是1
两向量的夹角为120°,模都是1∴|
 +t
+t |2=t2-t+1=
|2=t2-t+1=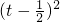 +
+ ,t∈R
,t∈R∴当t=
 时,|
时,| +t
+t |2取到最小值
|2取到最小值
∴|
 +t
+t |的最小值是
|的最小值是
故答案为

点评:本题考查平面向量的模的求法,向量数量积的运算,二次函数的最值,涉及到的知识点较多,解题的关键是理解题意,确定解题的方向为先求|
 +t
+t |2(t∈R)的最小值,向量求模常采用的技巧就是求模的平方.本题通过二次函数求最值,用到了函数的思想,这是最值问题常用的转化方向
|2(t∈R)的最小值,向量求模常采用的技巧就是求模的平方.本题通过二次函数求最值,用到了函数的思想,这是最值问题常用的转化方向 
练习册系列答案
相关题目
 ,
, ,分别从集合
,分别从集合 和
和 中随机取一个数
中随机取一个数 和
和 .
. ,求向量
,求向量 与
与 的夹角为锐角的概率;
的夹角为锐角的概率; ,则点
,则点 上为事件
上为事件
 ,
, 的概率最大的
的概率最大的 .
.