Question

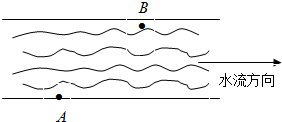
如图,一条河的两岸平行,河的宽度d=500 m.一艘船从A出发航行到河对岸,船航行的速度|v₁|=10 km/h,水流速度|v₂|=4 km/h,设v₁和v₂的夹角为θ(0＜θ＜π).

(1)当θ多大时,船能垂直到达对岸(即船的实际速度v=v₁+v₂与河岸垂直)?(精确到1°,可利用计算器计算)

(2)当船垂直到达对岸时,航行所需时间最少吗?为什么?

Answer 1

解:(1)船垂直到达对岸,即v=v₁+v₂与v₂垂直,即(v₁+v₂)·v₂=0.

∴v₁·v₂+v₂²=0,

即|v₁||v₂|cosθ+|v₂|²=0.

∴10×4cosθ+16=0.故cosθ=-.

又∵0°＜θ＜180°,

由计算器计算得θ=114°,

∴当θ=114°时,船垂直到达对岸.

(2)设当v₁与v₂夹角为θ(0°＜θ＜180°)时,船航行到对岸所需的时间为t,

则t=.

∴当θ=90°时,船的航行时间最短,而当船垂直到达对岸时,须有θ=114°,这时所需时间不是最少.