题目内容
已知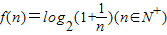 ,对正整数k,如果f(n)满足:f(1)+f(2)+f(3)+…+f(k+1)为整数,则称k为“好数”,那么区间[1,129]内所有“好数”的和S= .
,对正整数k,如果f(n)满足:f(1)+f(2)+f(3)+…+f(k+1)为整数,则称k为“好数”,那么区间[1,129]内所有“好数”的和S= .
【答案】分析:由题设知k=2n-2,再由2n-1≤129,解得1≤n≤7,故[1,129]内所有“好数”的和S=(2-2)+(22-2)+(23-2)+…+(27-2),由此能求出结果.
解答:解:∵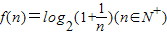 ,
,
∴f(1)=log22=1,
f(1)+f(2)+f(3)=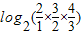 =log24=2,
=log24=2,
f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)
=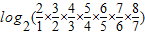 =log28=3.
=log28=3.
…
由题设知k=2n-2,
由2n-1≤129,解得1≤n≤7,
∴[1,129]内所有“好数”的和
S=(2-2)+(22-2)+(23-2)+…+(27-2)
=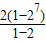 -14=240.
-14=240.
故答案为:240.
点评:本题考查数列的前n项和的求法,解题的关键是利用题设条件推导出[1,129]内所有“好数”的和S=(2-2)+(22-2)+(23-2)+…+(27-2).
解答:解:∵
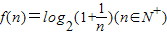 ,
,∴f(1)=log22=1,
f(1)+f(2)+f(3)=
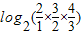 =log24=2,
=log24=2,f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+f(7)
=
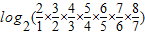 =log28=3.
=log28=3.…
由题设知k=2n-2,
由2n-1≤129,解得1≤n≤7,
∴[1,129]内所有“好数”的和
S=(2-2)+(22-2)+(23-2)+…+(27-2)
=
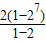 -14=240.
-14=240.故答案为:240.
点评:本题考查数列的前n项和的求法,解题的关键是利用题设条件推导出[1,129]内所有“好数”的和S=(2-2)+(22-2)+(23-2)+…+(27-2).

练习册系列答案
相关题目
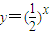 的图象上,且数列{an} 是a1=1,公差为d的等差数列.
的图象上,且数列{an} 是a1=1,公差为d的等差数列.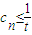 (t∈R,t≠0)对一切正整数n恒成立;
(t∈R,t≠0)对一切正整数n恒成立;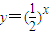 的图象上,且数列{an} 是a1=1,公差为d的等差数列.
的图象上,且数列{an} 是a1=1,公差为d的等差数列.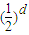 的等比数列;
的等比数列;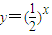 的图象上,且数列{an} 是a1=1,公差为d的等差数列.
的图象上,且数列{an} 是a1=1,公差为d的等差数列.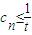 (t∈R,t≠0)对一切正整数n恒成立;
(t∈R,t≠0)对一切正整数n恒成立;