题目内容
(中线性运算)在平面直角坐标系中,若O为坐标原点,则A、B、C三点在同一直线上的充要条件为存在唯一的实数λ,使得
=λ•
+(1-λ)•
成立,此时称实数λ为“向量
关于
和
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
与向量a=(1,1)垂直,则“向量
关于
和
的终点共线分解系数”为( )
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OP3 |
| OP3 |
| OP1 |
| OP2 |
| A.-3 | B.3 | C.1 | D.-1 |
由
与向量
=(1,1)垂直,
可设
=(t,-t)(t≠0),
由
=λ•
+(1-λ)•
得(t,-t)=λ(1,3)+(1-λ)(-1,3)
=(4λ-1,3-2λ),
∴
,
两式相加得2λ+2=0,
∴λ=-1.
故选D
| OP3 |
| a |
可设
| OP3 |
由
| OP3 |
| OP1 |
| OP2 |
得(t,-t)=λ(1,3)+(1-λ)(-1,3)
=(4λ-1,3-2λ),
∴
|
两式相加得2λ+2=0,
∴λ=-1.
故选D

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
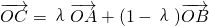 成立,此时称实数λ为“向量
成立,此时称实数λ为“向量 关于
关于 和
和 的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量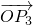 与向量a=(1,1)垂直,则“向量
与向量a=(1,1)垂直,则“向量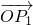 和
和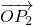 的终点共线分解系数”为
的终点共线分解系数”为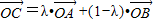 成立,此时称实数λ为“向量
成立,此时称实数λ为“向量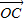 关于
关于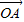 和
和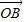 的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量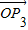 与向量a=(1,1)垂直,则“向量
与向量a=(1,1)垂直,则“向量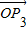 关于
关于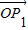 和
和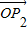 的终点共线分解系数”为( )
的终点共线分解系数”为( )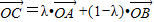 成立,此时称实数λ为“向量
成立,此时称实数λ为“向量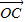 关于
关于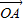 和
和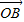 的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量
的终点共线分解系数”.若已知P1(3,1)、P2(-1,3),且向量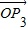 与向量a=(1,1)垂直,则“向量
与向量a=(1,1)垂直,则“向量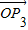 关于
关于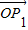 和
和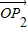 的终点共线分解系数”为( )
的终点共线分解系数”为( )