题目内容
如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且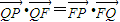 .
.(1)求动点P的轨迹C的方程;
(2)(文)过轨迹C的准线与y轴的交点M作方向向量为
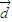 =(a,1)的直线m′与轨迹C交于不同两点A、B,问是否存在实数a使得FA⊥FB?若存在,求出a的范围;若不存在,请说明理由;
=(a,1)的直线m′与轨迹C交于不同两点A、B,问是否存在实数a使得FA⊥FB?若存在,求出a的范围;若不存在,请说明理由;(3)(文)在问题(2)中,设线段AB的垂直平分线与y轴的交点为D(0,y),求y的取值范围.
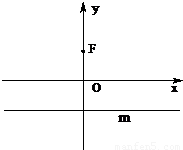
【答案】分析:(1)设P(x,y),由题意,Q(x,-1),利用向量的运算即可得出;
(2)由(1)可知:轨迹C为抛物线,准线方程为y=-1,即直线m,所以M(0,-1),当a=0时,直线m'的方程为x=0,与曲线C只有一个公共点,故a≠0.把直线m'的方程与抛物线的方程联立,利用判别式△、根与系数的关系、向量的运算FA⊥FB? ,即可得出a;
,即可得出a;
(3)由(2),得线段AB的中点为 ,线段AB的垂直平分线的一个法向量为
,线段AB的垂直平分线的一个法向量为 ,即可得到线段AB的垂直平分线的方程,利用(2)的a的取值范围即可得出.
,即可得到线段AB的垂直平分线的方程,利用(2)的a的取值范围即可得出.
解答:解:(1)设P(x,y),由题意,Q(x,-1),
 ,
, ,
, ,
, ,
,
由 ,得2(y+1)=x2-2(y-1),
,得2(y+1)=x2-2(y-1),
化简得x2=4y.所以,动点P的轨迹C的方程为x2=4y.
(2)轨迹C为抛物线,准线方程为y=-1,即直线m,所以M(0,-1),
当a=0时,直线m'的方程为x=0,与曲线C只有一个公共点,故a≠0.
所以直线m'的方程为 ,由
,由 得a2y2+(2a2-4)y+a2=0,
得a2y2+(2a2-4)y+a2=0,
由△=4(a2-2)2-4a4>0,得0<a2<1.
设A(x1,y1),B(x2,y2),则 ,y1y2=1,
,y1y2=1,
所以 ,x1x2=4,
,x1x2=4,
若FA⊥FB,则 ,即(x1,y1-1)•(x2,y2-1)=0,x1x2+y1y2-(y1+y2)+1=0,
,即(x1,y1-1)•(x2,y2-1)=0,x1x2+y1y2-(y1+y2)+1=0, ,
,
解得.所以 .
.
(3)由(2),得线段AB的中点为 ,
,
线段AB的垂直平分线的一个法向量为 ,
,
所以线段AB的垂直平分线的方程为 ,
,
令x=0, ,
,
因为0<a2<1,所以 .
.
所以y的取值范围是(3,+∞).
点评:本题主要考查抛物线的方程与性质、向量的运算及其数量积、直线与抛物线的位置关系、线段的垂直平分线等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想.
(2)由(1)可知:轨迹C为抛物线,准线方程为y=-1,即直线m,所以M(0,-1),当a=0时,直线m'的方程为x=0,与曲线C只有一个公共点,故a≠0.把直线m'的方程与抛物线的方程联立,利用判别式△、根与系数的关系、向量的运算FA⊥FB?
 ,即可得出a;
,即可得出a;(3)由(2),得线段AB的中点为
 ,线段AB的垂直平分线的一个法向量为
,线段AB的垂直平分线的一个法向量为 ,即可得到线段AB的垂直平分线的方程,利用(2)的a的取值范围即可得出.
,即可得到线段AB的垂直平分线的方程,利用(2)的a的取值范围即可得出.解答:解:(1)设P(x,y),由题意,Q(x,-1),
 ,
, ,
, ,
, ,
,由
 ,得2(y+1)=x2-2(y-1),
,得2(y+1)=x2-2(y-1),化简得x2=4y.所以,动点P的轨迹C的方程为x2=4y.
(2)轨迹C为抛物线,准线方程为y=-1,即直线m,所以M(0,-1),
当a=0时,直线m'的方程为x=0,与曲线C只有一个公共点,故a≠0.
所以直线m'的方程为
 ,由
,由 得a2y2+(2a2-4)y+a2=0,
得a2y2+(2a2-4)y+a2=0,由△=4(a2-2)2-4a4>0,得0<a2<1.
设A(x1,y1),B(x2,y2),则
 ,y1y2=1,
,y1y2=1,所以
 ,x1x2=4,
,x1x2=4,若FA⊥FB,则
 ,即(x1,y1-1)•(x2,y2-1)=0,x1x2+y1y2-(y1+y2)+1=0,
,即(x1,y1-1)•(x2,y2-1)=0,x1x2+y1y2-(y1+y2)+1=0, ,
,解得.所以
 .
.(3)由(2),得线段AB的中点为
 ,
,线段AB的垂直平分线的一个法向量为
 ,
,所以线段AB的垂直平分线的方程为
 ,
,令x=0,
 ,
,因为0<a2<1,所以
 .
.所以y的取值范围是(3,+∞).
点评:本题主要考查抛物线的方程与性质、向量的运算及其数量积、直线与抛物线的位置关系、线段的垂直平分线等基础知识,考查运算能力、推理论证以及分析问题、解决问题的能力,考查数形结合、化归与转化思想.

练习册系列答案
相关题目
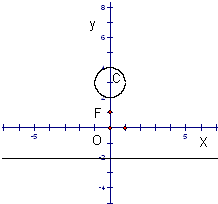 如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1.
如图,已知点F(0,1),直线L:y=-2,及圆C:x2+(y-3)2=1. (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且 (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且