Question

【题目】对定义在上的函数和常数，，若恒成立，则称为函数的一个“凯森数对”.

（1）若是的一个“凯森数对”，且，求；

（2）已知函数与的定义域都为，问它们是否存在“凯森数对”？分别给出判断并说明理由；

（3）若是的一个“凯森数对”，且当时，，求在区间上的不动点个数（函数的不动点即为方程的解）.

Answer 1

【答案】（1）7；（2）存在“凯森数对”，不存在“凯森数对”；（3）0.

【解析】

（1）由定义有，因此由这个递推式由已知可依次计算出；

（2）根据新定义对两个函数分别判断；

（3）求出时，的解析式，然后解方程，此方程在上无解，从而无不动点，由此可得在上无不动点．

（1）由题意，∵，∴，，，；

（2）设是的一个“凯森数对”，则，即，由于是上的任意实数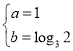，∴，∴存在“凯森数对”，

设是的一个“凯森数对”，则，对确定的，此等式最多有两个使它能成立，不可能对上的任意实数都成立，∴不存在“凯森数对”．

（3）根据新定义，，

当（）时，，

，

由，得，解得或，均不属于，

即在上无不动点．

由于，

∴在上无不动点．不动点个数为0.