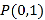题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
(1)以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,求曲线
轴的非负半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和点
的极坐标方程和点![]() 的极坐标;
的极坐标;
(2)若点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
【答案】(1) ![]() ;点
;点![]() 的极坐标为
的极坐标为![]() 或
或![]() .(2)
.(2) ![]()
【解析】
(1)由![]() 得
得![]() 得曲线
得曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,结合图象可求得
,结合图象可求得![]() 的极径和角,可得
的极径和角,可得![]() 的极坐标;
的极坐标;
(2)不妨取![]() ,设
,设![]() ,根据面积公式
,根据面积公式![]() 以及三角函数的性质可得最大值.
以及三角函数的性质可得最大值.
解(1)由![]() 得
得![]()
故曲线![]() 的极坐标方程为
的极坐标方程为![]() ,即
,即![]() ,
,
如图:当![]() 与圆相切时,
与圆相切时,![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴点![]() 的极坐标为
的极坐标为![]() 或
或![]() .
.
(2)由于圆、点![]() 、点
、点![]() 均关于
均关于![]() 轴对称,
轴对称,
故不论点A在何处,都不会影响![]() 面积最大值的取得.
面积最大值的取得.
不妨取![]() ,设
,设![]() ,
,
则![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 时,面积取得最大值
时,面积取得最大值![]() .
.

练习册系列答案
相关题目
【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,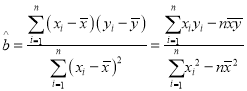 ,
,![]() 为数据平均数)
为数据平均数)