题目内容
(2012•黄州区模拟)观察下列等式:
×
=1-
,
×
+
×
=1-
,
×
+
×
+
×
=1-
,…,由以上等式推测到一个一般结论为:
×
+
×
+
×
+…+
×
=1-
(n∈N*)
×
+
×
+
×
+…+
×
=1-
(n∈N*).
| 3 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 1 |
| 3×22 |
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 5 |
| 3×4 |
| 1 |
| 23 |
| 1 |
| 4×23 |
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 5 |
| 3×4 |
| 1 |
| 23 |
| n+2 |
| n(n+1)2n |
| 1 |
| 2n |
| 1 |
| (n+1)2n |
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 5 |
| 3×4 |
| 1 |
| 23 |
| n+2 |
| n(n+1)2n |
| 1 |
| 2n |
| 1 |
| (n+1)2n |
分析:由已知中的三个式子,我们分析等式左边每一个累加项的变化趋势,可以归纳出其通项为
,分析等式右边的式子,发现每一个式了均为两项差的形式,且被减数均为1,减数为
,由此即可得到结论.
| n+2 |
| n(n+1) |
| 1 |
| (n+1)2 n |
解答:解:由已知中的等式,
×
=1-
,
×
+
×
=1-
,
×
+
×
+
×
=1-
,
…,
我们可以推断:
对于n∈N*,
×
+
×
+
×
+…+
×
=1-
.
故答案为:
×
+
×
+
×
+…+
×
=1-
(n∈N*).
| 3 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 1 |
| 3×22 |
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 5 |
| 3×4 |
| 1 |
| 23 |
| 1 |
| 4×23 |
…,
我们可以推断:
对于n∈N*,
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 5 |
| 3×4 |
| 1 |
| 23 |
| n+2 |
| n(n+1)2n |
| 1 |
| 2n |
| 1 |
| (n+1)2n |
故答案为:
| 3 |
| 1×2 |
| 1 |
| 2 |
| 4 |
| 2×3 |
| 1 |
| 22 |
| 5 |
| 3×4 |
| 1 |
| 23 |
| n+2 |
| n(n+1)2n |
| 1 |
| 2n |
| 1 |
| (n+1)2n |
点评:本题考查的知识点是归纳推理,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
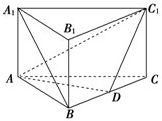 (2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点.
(2012•黄州区模拟)如图,在直三棱柱ABC-A1B1C1中,AB=BC=2AA1,∠ABC=90°,D是BC的中点. (2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为
(2012•黄州区模拟)已知某几何体的三视图如图,则该几何体的表面积为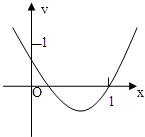 (2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )
(2012•黄州区模拟)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=2lnx+f(x)在点(b,g(b))处切线的斜率的最小值是( )