题目内容
用二分法求函数y=x3-3的一个正零点（精确度0.1）．
解：由于f（1）=-2＜0，f（2）=5＞0，因此可取区间[1，2]作为计算的初始区间，用二分法逐次计算，见下表：
续表
从表中可知|1.5-1.437 5|=0.062 5＜0.1，
所以函数y=x3-3精确度为0.1的零点，可取为1.5或1.4375．
分析：计算可得f（1）=-2＜0，f（2）=5＞0，根据零点存在定理可取区间[1，2]作为计算的初始区间，用二分法逐次计算，直到区间端点的差精确度0.1即可．
点评：本题考查的知识点是二分法求方程的近似解，其中熟练掌握二分法的方法，是解答本题的关键，属于中档题．
| 端点或中点坐标 | 端点或中点的函数值 | 取区间 |
| a0=1，b0=2 | f（1）=-2＜0，f（2）=5＞0 | （1，2） |
x1= =1.5 | f（1.5）=0.375＞0 | （1，1.5） |
x2= =1.25 | f（1.25）=-1.04 69＜0 | （1.25，1.5） |
x3= =1.375 | f（1.375）=-0.400 4＜0 | （1.375，1.5） |
x4= =1.437 5 | f（1.437 5）=-0.029 5＜0 | （1.437 5，1.5） |
所以函数y=x3-3精确度为0.1的零点，可取为1.5或1.4375．
分析：计算可得f（1）=-2＜0，f（2）=5＞0，根据零点存在定理可取区间[1，2]作为计算的初始区间，用二分法逐次计算，直到区间端点的差精确度0.1即可．
点评：本题考查的知识点是二分法求方程的近似解，其中熟练掌握二分法的方法，是解答本题的关键，属于中档题．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
＝3，计算得f(2)·f(x1)<0，则此时零点x0所在的区间是 ( )
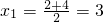，计算得f（2）•f（x1）＜0，则此时零点x0∈________．（填区间）