题目内容
【题目】已知函数![]() (
(![]() ).
).
(1)若![]() 为
为![]() 的极值点,求实数
的极值点,求实数![]() 的值;
的值;
(2)若![]() 在
在![]() 上是单调增函数,求实数
上是单调增函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,方程
时,方程![]() 有实根,求实数
有实根,求实数![]() 的最大值.
的最大值.
【答案】(1)0;(2)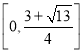 ;(3)0.
;(3)0.
【解析】
(1)根据![]() 建立关于a的方程求出a的值.
建立关于a的方程求出a的值.
(2)本小题实质是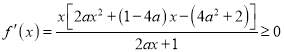 在区间
在区间![]() 上恒成立,
上恒成立,
进一步转化为![]() 在区间
在区间![]() 上恒成立,
上恒成立,
然后再讨论a=0和![]() 两种情况研究.
两种情况研究.
(2)![]() 时,方程
时,方程![]() 可化为,
可化为,![]() ,
,
问题转化为![]() 在
在![]() 上有解,
上有解,
利用导数研究g(x)的单调区间极值最值,从而求出值域,问题得解.
(1)![]()
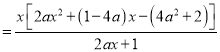 .
.
因为![]() 为
为![]() 的极值点,所以
的极值点,所以![]() .
.
即![]() ,解得
,解得![]() .
.
又当![]() 时,
时,![]() ,从而
,从而![]() 的极值点成立.
的极值点成立.
(2)因为![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以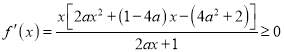 在区间
在区间![]() 上恒成立.
上恒成立.
①当![]() 时,
时,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 上为增函数,故
上为增函数,故![]() ,符合题意.
,符合题意.
②当![]() 时,由函数
时,由函数![]() 的定义域可知,必须有
的定义域可知,必须有![]() 对
对![]() 恒成立,故只能
恒成立,故只能![]() ,所以
,所以![]() 对
对
![]() 上恒成立.
上恒成立.
令![]() ,其对称轴为
,其对称轴为![]() ,
,
因为![]() 所以
所以![]() ,从而
,从而![]() 上恒成立,只要
上恒成立,只要![]() 即可,
即可,
因为![]()
![]() ,
,
解得![]() .因为
.因为![]() ,所以
,所以![]() .
.
综上所述,![]() 的取值范围为
的取值范围为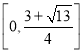 .
.
(3)若![]() 时,方程
时,方程![]() 可化为,
可化为,![]() .
.
问题转化为![]() 在
在![]() 上有解,
上有解,
即求函数![]() 的值域.
的值域.
因为![]() ,令
,令![]() ,
,
则![]() ,
,
所以当![]() 时,
时,![]() ,从而
,从而![]() 在
在![]() 上为增函数,
上为增函数,
当![]() 时,
时,![]() ,从而
,从而![]() 在
在![]() 上为减函数,
上为减函数,
因此![]() .
.
而![]() ,故
,故![]() ,
,
因此当![]() 时,
时,![]() 取得最大值0.
取得最大值0.

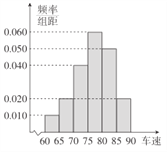
【题目】已知学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学). 现用分层抽样方法(按A类、B类分两层)从该年级学生中共抽查100名同学,测得这100名同学的身高(单位:![]() )频率分布直方图如图:
)频率分布直方图如图:
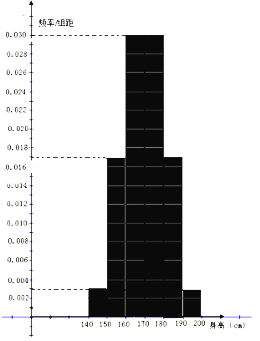
(Ⅰ)以同一组数据常用该组区间的中点值(例如区间![]() 的中点值为165)作为代表,计算这100名学生身高数据的平均值;
的中点值为165)作为代表,计算这100名学生身高数据的平均值;
(Ⅱ)如果以身高不低于![]() 作为达标的标准,对抽取的100名学生,得到以下列联表:
作为达标的标准,对抽取的100名学生,得到以下列联表:
身高达标 | 身高不达标 | 总计 | |
积极参加体育锻炼 | 40 | ||
不积极参加体育锻炼 | 15 | ||
总计 | 100 |
完成上表,并判断是否有![]() 的把握认为体育锻炼与身高达标有关系(
的把握认为体育锻炼与身高达标有关系(![]() 值精确到0.01)?
值精确到0.01)?
参考公式: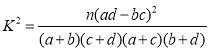
参考数据:
|
|
|
|
|
|
|
|
|
|