题目内容
已知定义在实数集R上的奇函数f(x)有最小正周期2,且当x∈(0,1)时, .
.(1)证明f(x)在(0,1)上为减函数;
(2)求函数f(x)在[-1,1]上的解析式;
(3)当λ取何值时,方程f(x)=λ在R上有实数解.
【答案】分析:(1)利用函数单调性的定义证明.(2)利用函数的周期性和奇偶性求对应的解析式.(3)利用函数的性质求函数f(x)的值域即可.
解答:解:(1)证明:设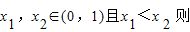 ,
,
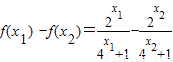 =
=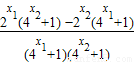 =
=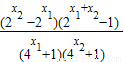 …(3分)
…(3分)
∵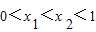 ,∴
,∴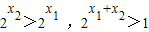
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(0,1)上为减函数.…(4分)
(2)若x∈(-1,0)∴-x∈(0,1),∴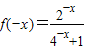 ,
,
又∵f(x)为奇函数,∴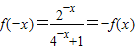 ∴
∴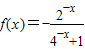 …(6分)
…(6分)
又∵f(-1)=f(1),且f(-1)=-f(1)∴f(1)=f(-1)=0
∴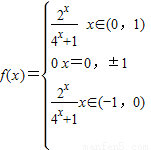 …(8分)
…(8分)
(3)若x∈(0,1),∴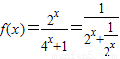
又∵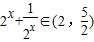 ,∴
,∴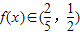 ,…(10分)
,…(10分)
若x∈(-1,0),∴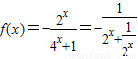 ∴
∴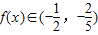 ,
,
∴λ的取值范围是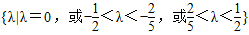 .…12 分
.…12 分
点评:本题主要考查函数奇偶性和单调性的应用和证明,要求熟练掌握函数性质的综合应用.
解答:解:(1)证明:设
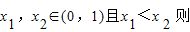 ,
,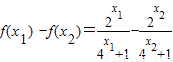 =
=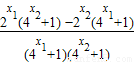 =
=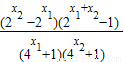 …(3分)
…(3分)∵
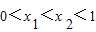 ,∴
,∴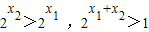
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在(0,1)上为减函数.…(4分)
(2)若x∈(-1,0)∴-x∈(0,1),∴
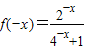 ,
,又∵f(x)为奇函数,∴
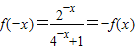 ∴
∴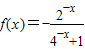 …(6分)
…(6分)又∵f(-1)=f(1),且f(-1)=-f(1)∴f(1)=f(-1)=0
∴
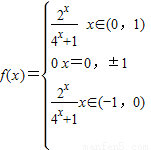 …(8分)
…(8分)(3)若x∈(0,1),∴
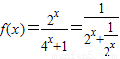
又∵
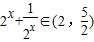 ,∴
,∴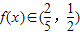 ,…(10分)
,…(10分)若x∈(-1,0),∴
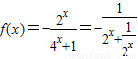 ∴
∴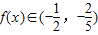 ,
,∴λ的取值范围是
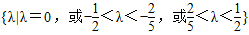 .…12 分
.…12 分点评:本题主要考查函数奇偶性和单调性的应用和证明,要求熟练掌握函数性质的综合应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 已知定义在实数集R上的奇函数f(x),当x>0时,f(x)的图象是抛物线的一部分,且该抛物线经过点(1,0)、(3,0)和(0,3).
已知定义在实数集R上的奇函数f(x),当x>0时,f(x)的图象是抛物线的一部分,且该抛物线经过点(1,0)、(3,0)和(0,3).