题目内容
已知全集U=R,A={x|x2-2x-8<0},B={x||x+3|>2},C={x|x2-4ax+3a2<0}.(1)C![]() (A∩B),求a的取值范围;
(A∩B),求a的取值范围;
(2)C![]() (
(![]() A)∩(
A)∩(![]() B),求a的取值范围.
B),求a的取值范围.
解析:A={x|-2<x<4},
B={x|x>-1或x<-5}.
∴A∩B={x|-1<x<4}.
当a>0时,C={x|a<x<3a};
当a=0时,C=![]() ;
;
当a<0时,C={x|3a<x<a}.
(1)若C![]() A∩B,则
A∩B,则
a=0或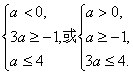
∴a∈[-![]() ].
].
(2)(![]() A)∩(
A)∩(![]() B)={x|-5≤x≤-2}.
B)={x|-5≤x≤-2}.
若C![]() (
(![]() A)∩(
A)∩(![]() B),则
B),则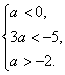
∴-2<a<-![]() ,即a∈(-2,-
,即a∈(-2,-![]() ).
).

练习册系列答案
相关题目