题目内容
在下列四个函数中，满足性质：“对于区间（1，2）上的任意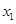
,
(
). 
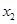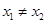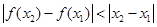恒成立”的只有（ ）
A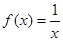． | B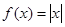． | C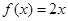． | D． |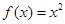
A
解析
练习册系列答案
阅读快车系列答案
相关题目
f(x)是定义在R上的增函数,则不等式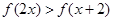
的解集是（ ）
| A．(0 ,+∞) | B．(0 , 2) | C．(2 ,+∞) | D．(-∞，2) |
的图象的大致形状是（ ）
如果奇函数
在区间
上是增函数，且最小值为
，那么在区间
上是
| A．增函数且最小值为 | B．增函数且最大值为 |
| C．减函数且最小值为 | D．减函数且最大值为 |
，
，给出如下四个图形，其中能表
到集合
的函数关系的是 ( )
“函数
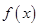在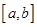
上单调”是“函数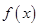在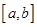上有最大值和最小值”的（ ）条件.
| A．充分但不必要 | B．必要但不充分 |
| C．充分必要 | D．既不充分也不必要 |
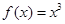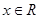若函数
(
)，则函数
在其定义域上是
| A．单调递减的偶函数 | B．单调递减的奇函数 |
| C．单凋递增的偶函数 | D．单调递增的奇函数 |
定义在R上的函数f(x)满足f(x)=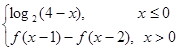 
，则f（3）的值
为( )
| A．-1 | B．-2 | C．1 | D．2 |
函数y=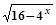
的值域是 （ ）
| A．[0,+∞） | B．（0,4] | C．[0,4） | D．（0,4） |