Question

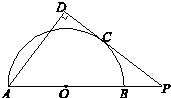（2013•石景山区二模）如图，AB是半圆O的直径，P在AB的延长线上，PD与半圆O相切于点C，AD⊥PD．若PC=4，PB=2，则CD=

12

5

．

Answer 1

分析：由PD与半圆O相切于点C及切割线定理得PC²=PB•PA，OC⊥PD．再利用AD⊥PD得到OC∥AD．利用平行线分线段成比例即可得出．

解答：解：设圆的半径为R．连接OC．
∵PD与半圆O相切于点C，∴PC²=PB•PA，OC⊥PD．．
∵PC=4，PB=2，
∴4²=2×（2+2R），
解得R=3．
又∵AD⊥PD，∴OC∥AD．
∴

PC

CD

=

PO

OA

．
∴

4

CD

=

2+3

3

，解得CD=

12

5

．
故答案为

12

5

．

点评：熟练掌握圆的切线的性质、切割线定理、平行线分线段成比例定理是解题的关键．