题目内容
已知椭圆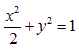 ,
,
(1)求斜率为2的平行弦的中点轨迹方程。
(2)过A(2,1)的直线L与椭圆相交,求L被截得的弦的中点轨迹方程;
(3)过点P(0.5,0.5)且被P点平分的弦所在直线的方程。
(1)y=![]() ;
;
(2)![]() (去除包含在椭圆
(去除包含在椭圆 内部的部分);
内部的部分);
(3)2x+4y-3=0。
解析:
(1)设这些平行弦的方程为y=2x+m,弦的中点为M(x,y).
联立直线方程和椭圆方程:y=2x+m, 消去y得,
消去y得,
![]() ,
,
因此![]() =-
=-![]() ,
,![]() .
.
M的坐标是:x=![]() ,y=2x+m,
,y=2x+m,![]() ,消去m得:y=
,消去m得:y=![]() .
.
(2)设弦的端点为P(![]() ),Q(
),Q(![]() ),其中点是M(x,y).
),其中点是M(x,y).

![]() 因此:
因此:![]() =
=![]() ,
,
化简得:![]() (去除包含在椭圆
(去除包含在椭圆 内部的部分).
内部的部分).
(3)由(2)可得弦所在直线的斜率为k=![]() =
=![]() ,因此所求直线方程是:
,因此所求直线方程是:
y-![]() =-
=-![]() (x-
(x-![]() ),化简得:2x+4y-3=0.
),化简得:2x+4y-3=0.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 .
. )且被P点平分的弦所在的直线方程.
)且被P点平分的弦所在的直线方程.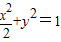 .
.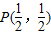 且被点P平分的弦所在直线的方程;
且被点P平分的弦所在直线的方程;