题目内容
选做题
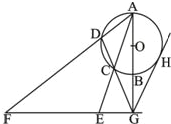
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过G作⊙O的切线,切点为H.求证:
(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE•GF.
如图所示,AB是⊙O的直径,G为AB延长线上的一点,GCD是⊙O的割线,过点G作AB的垂线,交AC的延长线于点E,交AD的延长线于点F,过G作⊙O的切线,切点为H.求证:
(Ⅰ)C,D,F,E四点共圆;
(Ⅱ)GH2=GE•GF.


证明:(Ⅰ)连接BC.∵AB是⊙O的直径,∴∠ACB=90°.∵AG⊥FG,
∴∠AGE=90°.又∠EAG=∠BAC,∴∠ABC=∠AEG.又∠FDC=∠ABC,
∴∠FDC=∠AEG.∴∠FDC+∠CEF=180°.
∴C,D,F,E四点共圆.(5分)
(Ⅱ)∵GH为⊙O的切线,GCD为割线,∴GH2=GC•GD.
由C,D,F,E四点共圆,得∠GCE=∠AFE,∠GEC=∠GDF.
∴△GCE∽△GFD.∴
| GC |
| GF |
| GF |
| GD |
∴CH2=GE•GF.(10分)

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 选做题
选做题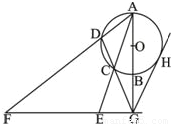 选做题
选做题 选做题
选做题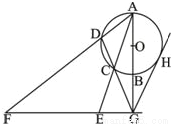 选做题
选做题