题目内容
17、设a∈R且a≠2,函数f(x)=ex(x2-ax+a).
(1)求f'(0)的值;
(2)求函数f(x)的单调区间.
(1)求f'(0)的值;
(2)求函数f(x)的单调区间.
分析:(1)首先求出f′(x),然后令x=0求出f′(0)的值,
(2)首先求出函数的导数,令f′(x)=0,解出函数的极值点,最后根据导数判断函数的单调性,从而求解.
(2)首先求出函数的导数,令f′(x)=0,解出函数的极值点,最后根据导数判断函数的单调性,从而求解.
解答:解:(Ⅰ)f′(x)=(ex)′(x2-ax+a)+ex(x2-ax+a)′
=ex(x2-ax+a)+ex(2x-a)
=ex[x2-(a-2)x]
=exx[x-(a-2)]
∴f′(0)=0,
(Ⅱ)令f′(x)=0,
解得x1=0,x2=a-2,
∵函数f(x)定义域为R,且对任意x∈R,ex>0,
∴当a-2>0,即a>2时,

所以f(x)的单调递增区间是(-∞,0),(a-2,+∞),单调递减区间是(0,a-2).
当a-2<0,即a<2时,

所以f(x)的单调递增区间是(-∞,a-2)∪(0,+∞),单调递减区间是(a-2,0).
综上,当a>2时,f(x)的单调递增区间是(-∞,0)∪(a-2,+∞),单调递减区间是(0,a-2),
当a<2时,f(x)的单调递增区间是(-∞,a-2)∪(0,+∞),单调递减区间是(a-2,0).
=ex(x2-ax+a)+ex(2x-a)
=ex[x2-(a-2)x]
=exx[x-(a-2)]
∴f′(0)=0,
(Ⅱ)令f′(x)=0,
解得x1=0,x2=a-2,
∵函数f(x)定义域为R,且对任意x∈R,ex>0,
∴当a-2>0,即a>2时,

所以f(x)的单调递增区间是(-∞,0),(a-2,+∞),单调递减区间是(0,a-2).
当a-2<0,即a<2时,

所以f(x)的单调递增区间是(-∞,a-2)∪(0,+∞),单调递减区间是(a-2,0).
综上,当a>2时,f(x)的单调递增区间是(-∞,0)∪(a-2,+∞),单调递减区间是(0,a-2),
当a<2时,f(x)的单调递增区间是(-∞,a-2)∪(0,+∞),单调递减区间是(a-2,0).
点评:此题主要考查函数导数与函数单调性之间的关系,需要掌握并会熟练运用导数与函数单调性的关系.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
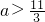 ;
;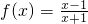 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集. ;
;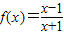 ,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.
,设f2(x)=f[f(x)],f3(x)=f[f2(x)],…,fn+1(x)=f[fn(x)](n∈N*且n≥2),令集合M={x|f2009(x)=x,x∈R},则集合M为空集.