题目内容
已知数列{an}满足∵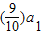
+
+…+
=
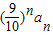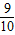（n2+3n）．（1）求数列{an}的通项公式；
（2）分析数列{an}有没有最大项，若有，求出这个最大项；若没有，说明理由．
【答案】分析：（1）再写一式，两式相减，即可求数列{an}的通项公式；
（2）确定数列{an}为递增数列，即可得到数列没有最大项．
解答：解：（1）∵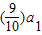
+
+…+
=
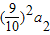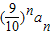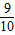（n2+3n）①
∴n≥2时，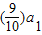
+
+…+
=
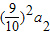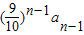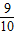[（n-1）2+3（n-1）]②
①-②可得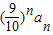
=
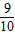（2n+2）
∴n≥2时，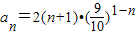
∵n=1时，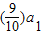
=
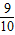×4，∴a1=4，满足上式
∴
；
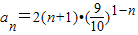（2）∵
=
=
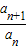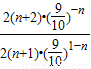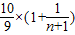＞1，an＞0
∴an+1＞an
∴数列{an}为递增数列，因此数列没有最大项．
点评：本题考查数列递推式，考查数列的通项，考查数列的单调性，考查学生的计算能力，属于中档题．
（2）确定数列{an}为递增数列，即可得到数列没有最大项．
解答：解：（1）∵
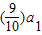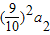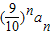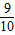++…+=（n2+3n）①∴n≥2时，
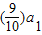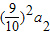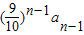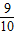++…+=[（n-1）2+3（n-1）]②①-②可得
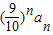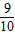=（2n+2）∴n≥2时，
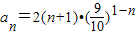
∵n=1时，
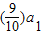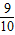=×4，∴a1=4，满足上式∴
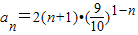；（2）∵
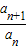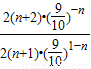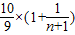==＞1，an＞0∴an+1＞an
∴数列{an}为递增数列，因此数列没有最大项．
点评：本题考查数列递推式，考查数列的通项，考查数列的单调性，考查学生的计算能力，属于中档题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目