题目内容
【题目】已知函数![]() ,记
,记![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(1)当![]() 时,求证:函数
时,求证:函数![]() 的图像(除切点外)均为切线
的图像(除切点外)均为切线![]() 的下方;
的下方;
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)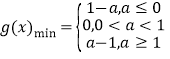
【解析】
(1)求得f(x)的导数,考虑极值点以及函数的凹凸性,即可得证;
(2)讨论a<0,a=0,a>1,a=1,0<a<1时,函数h(x)=f(x)﹣2lnx的导数和单调性,最值,即可得到所求g(x)的最小值.
(1)设切线方程为![]()
记![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”.
”.
故命题成立
(2)![]() .
.
设![]() ,
,![]() ,
,
1)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,且
上单调递减,且![]() .
.
∴![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
∴![]()
2)当![]() 时,
时,![]() ,
,
设![]() ,
,![]() ,
,![]() 有两根
有两根![]() ,
,![]() ,
,
![]() ,
,![]() ,不妨令
,不妨令![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
①当![]() ,即
,即![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,∴
,∴![]() ;
;![]()
②当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() ,
,
存在![]() 使得
使得![]() ,
,
∴![]() .
.
综上可得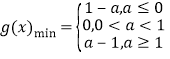 .
.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.
【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系,随机调查100名高一学生,得到![]() 列联表如下:由此得出的正确结论是( )
列联表如下:由此得出的正确结论是( )
选择物理 | 不选择物理 | 总计 | |
男 | 35 | 20 | 55 |
女 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
附: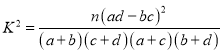
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别有关”
B.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别无关”
C.有![]() 的把握认为“选择物理与性别有关”
的把握认为“选择物理与性别有关”
D.有![]() 的把握认为“选择物理与性别无关”
的把握认为“选择物理与性别无关”