题目内容
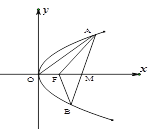
【题目】已知椭圆E的方程为![]() y2=1,其左焦点和右焦点分别为F1,F2,P是椭圆E上位于第一象限的一点
y2=1,其左焦点和右焦点分别为F1,F2,P是椭圆E上位于第一象限的一点
(1)若三角形PF1F2的面积为![]() ,求点P的坐标;
,求点P的坐标;
(2)设A(1,0),记线段PA的长度为d,求d的最小值.
【答案】(1)P(1,![]() ) (2)
) (2)![]()
【解析】
(1)设P(x,y);![]() ,根据三角形PF1F2的面积为
,根据三角形PF1F2的面积为![]() 列等式解得
列等式解得![]() ,再代入椭圆方程可得
,再代入椭圆方程可得![]() ,即可得到答案;
,即可得到答案;
(2)根据两点间的距离公式得到![]() 的函数关系式,再根据二次函数求最值可得结果.
的函数关系式,再根据二次函数求最值可得结果.
椭圆E的方程为![]() y2=1,其左焦点和右焦点分别为F1,F2,
y2=1,其左焦点和右焦点分别为F1,F2,
所以:椭圆的顶点坐标(±2,0);(0,±1),焦点:F1(![]() ,0),F2(
,0),F2(![]() ,0),
,0),
|F1F2|=2![]() ;
;
P是椭圆E上位于第一象限的一点,设P(x,y);![]() ;
;
(1)若三角形PF1F2的面积为![]() ,即:
,即:![]()
![]() |F1F2|×y
|F1F2|×y![]() ;
;
解得:y![]() ,
,
因为P是椭圆E上位于第一象限的一点,满足椭圆的方程,代入椭圆方程得:x=1,
所以:点P的坐标P(1,![]() );
);
(2)设A(1,0),记线段PA的长度为d,P是椭圆E上位于第一象限的一点,
所以:d![]() .
.
因为![]() ,所以
,所以![]()
![]() 时,d有最小值,
时,d有最小值,
所以d的最小值d![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目