题目内容
如图,在正三棱锥A—BCD中,E、F分别是AB、BC的中点,EF⊥DE,且BC=1,则正三棱锥A—BCD的体积是( )

A.  B.
B. C.
C.  D.
D. 
B
解析试题分析:EF⊥DE,EF∥AC∴AC⊥DE,又AC⊥BD∴AC⊥面ABD,
AB=AC=AD= ,可求体积:
,可求体积: ×
× ×
× ×
× ×
× =
=  。
。
故选B.
考点:本题主要考查三棱锥的几何特征,体积计算。
点评:典型题,先证明AC⊥面ABD,然后求底面ACD的面积,即可求出体积.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是
A.32 、 、 | B.16 、 、 |
C.12 、 、 | D.8 、 、 |
某几何体的三视图如图所示,则它的体积是( )
A.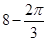 | B. |
C. | D. |
过空间任意一点引三条不共面的直线,它们所确定的平面个数是( )
| A.1 | B.2 | C.3 | D.1或3 |
几何体的三视图如图所示,则该几何体的体积为
| A.2π+2√3 | B.4π+2√3 |
| C.2π+2√3/3 | D.4π+2√3/3 |
若一个球的表面积为4 ,则这个球的体积是( )
,则这个球的体积是( )
A. | B. | C. | D. |



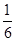
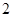 的正方形,两条虚线互相垂直,则该几何体的体积是( )
的正方形,两条虚线互相垂直,则该几何体的体积是( )




 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面 ,在折起后形成的三棱锥
,在折起后形成的三棱锥 中,给出下列三个命题:
中,给出下列三个命题: 是等边三角形; ②
是等边三角形; ② ; ③三棱锥
; ③三棱锥 .
.