题目内容
已知函数![]() 的图象过原点,
的图象过原点,![]() ,
,![]() ,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
(1)若y=F(x)在x=-1处取得极大值2,求函数y=F(x)的单调区间;
(2)若使g(x)=0的x值满足![]() ,求线段AB在x轴上的射影长的取值范围;
,求线段AB在x轴上的射影长的取值范围;
(I)F(x)的单调递减区间为[-1,1],单调递增区间为![]()
(II)![]()
解析:
![]() 的图象过原点则d=0
的图象过原点则d=0
![]() 。
。![]() (1)
(1)
(I)y=F(x)在x=-1处取得极大值2
![]() (2)
(2)
![]() (3)
(3)
由(1)(2)(3)得a=3, b=0, c=-3
![]()
由![]() 得
得![]()
由![]() 得
得![]()
∴F(x)的单调递减区间为[-1,1],单调递增区间为![]()
(II)![]()
![]()
由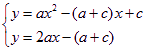 得
得![]()
设A(x1, y1),B(x2, y2)则![]()
线段AB在x轴上射影长![]()
由g(x)=0得![]()
由![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称. ,求数列an的通项公式an.
,求数列an的通项公式an. 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.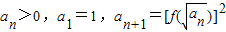 ,求数列an的通项公式an.
,求数列an的通项公式an.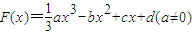 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B. ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.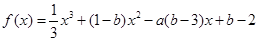 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组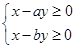 所确定的平面区域在
所确定的平面区域在 内的面积为 .
内的面积为 .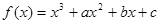 的图象过原点,且
的图象过原点,且 在
在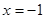 ,
, 处取得极值.
处取得极值.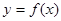 与
与 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.