题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,设向量 =(a,
=(a, ),
), =(cosC,c-2b),且
=(cosC,c-2b),且 ⊥
⊥ .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=1,求△ABC的周长l的取值范围.
解:(Ⅰ)由题意 ⊥
⊥ .可知:
.可知: ,
,
即acosC+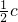 =b,得sinAcosC+
=b,得sinAcosC+ sinC=sinB.
sinC=sinB.
又sinB=sin(A+C)=sinAcosB+cosAsinC.
∴ ,∵sinC≠0,∴cosA=
,∵sinC≠0,∴cosA= .
.
又0<A<π∴A= .
.
(Ⅱ)由正弦定理得:b=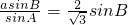 ,
, ,
,
l=a+b+c=1+ =1+
=1+
=1+2(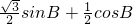 )
)
=1+2sin(B+ ).
).
∵A= .
.
∴B∈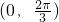 ,∴B+
,∴B+
 ,
,
∴sin(B+ )
) .
.
故△ABC的周长l的范围为(2,3].
分析:(Ⅰ)利用向量的垂直,推出数量积为0,通过三角形内角和以及两角和的正弦函数,确定角A的大小;
(Ⅱ)若a=1,利用正弦定理求出b、c的表达式,通过三角形的内角和以及两角和的正弦函数化简表达式,根据角的范围,确定三角函数的范围,然后求△ABC的周长l的取值范围.
点评:本题考查正弦定理,两角和的正弦函数,向量的数量积等知识的应用,考查计算能力.
 ⊥
⊥ .可知:
.可知: ,
,即acosC+
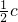 =b,得sinAcosC+
=b,得sinAcosC+ sinC=sinB.
sinC=sinB.又sinB=sin(A+C)=sinAcosB+cosAsinC.
∴
 ,∵sinC≠0,∴cosA=
,∵sinC≠0,∴cosA= .
.又0<A<π∴A=
 .
.(Ⅱ)由正弦定理得:b=
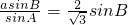 ,
, ,
,l=a+b+c=1+
 =1+
=1+
=1+2(
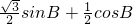 )
)=1+2sin(B+
 ).
).∵A=
 .
.∴B∈
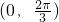 ,∴B+
,∴B+
 ,
,∴sin(B+
 )
) .
.故△ABC的周长l的范围为(2,3].
分析:(Ⅰ)利用向量的垂直,推出数量积为0,通过三角形内角和以及两角和的正弦函数,确定角A的大小;
(Ⅱ)若a=1,利用正弦定理求出b、c的表达式,通过三角形的内角和以及两角和的正弦函数化简表达式,根据角的范围,确定三角函数的范围,然后求△ABC的周长l的取值范围.
点评:本题考查正弦定理,两角和的正弦函数,向量的数量积等知识的应用,考查计算能力.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |