题目内容
已知函数
在区间（1，2）内是增函数，则实数m的取值范围是（ ）A．
B．
C．（0，1]
D．
【答案】分析：首先求出函数的导数，然后根据导数与函数增减性的关系求出m的范围．
解答：解：由题得f′（x）=x2-2mx-3m2=（x-3m）（x+m），
∵函数
在区间（1，2）内是增函数，
∴f′（x）＞0，
当m≥0时，3m≤1，
∴0≤m≤
，
当m＜0时，-m≤1，
∴-1≤m＜0，
∴m∈[-1，
]．
故选D．
点评：掌握函数的导数与单调性的关系．
解答：解：由题得f′（x）=x2-2mx-3m2=（x-3m）（x+m），
∵函数
在区间（1，2）内是增函数，∴f′（x）＞0，
当m≥0时，3m≤1，
∴0≤m≤
，当m＜0时，-m≤1，
∴-1≤m＜0，
∴m∈[-1，
]．故选D．
点评：掌握函数的导数与单调性的关系．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
在区间[－1，1]上最大值为1，最小值为－2。
的解析式；
在区间[－2，2]上为减函数，求实数m的取值范围。
在区间[0,1]上是减函数，则实数
的取值范围是 .
在区间[－1,1]上的最大值是14，求a的值.
在区间[－1,1]上的最大值是14，求a的值.
在区间[0,1]上是增函数，在区间（-∞，0），（1，+∞）上是减函数，又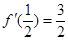
，
的解析式。
成立，求m的取值范围。