题目内容
已知A、B、C是直线l上的三点,向量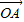 、
、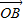 、
、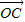 满足
满足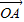 -(y+1-lnx)
-(y+1-lnx)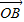 +
+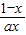
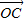 =
=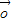 ,(O不在直线l上a>0)
,(O不在直线l上a>0)(1)求y=f(x)的表达式;
(2)若函数f(x)在[1,∞]上为增函数,求a的范围;
(3)当a=1时,求证lnn>
 +
+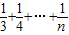 ,对n≥2的正整数n成立.
,对n≥2的正整数n成立.
【答案】分析:(1)将条件变形,利用A,B,C三点共线,可得(y+1-lnx)-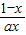 =1,从而可得结论;
=1,从而可得结论;
(2)函数f(x)在[1,+∞)上为增函数,等价于f′(x)≥0在[1,+∞)上恒成立,分离参数,即可求a的范围;
(3)先证明lnx≥1-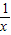 ,再将x用
,再将x用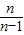 替代,即可证得结论.
替代,即可证得结论.
解答:(1)解:∵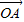 -(y+1-lnx)
-(y+1-lnx)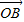 +
+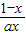
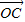 =
=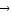 ,
,
∴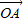 =(y+1-lnx)
=(y+1-lnx)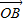 -
-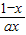
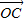 ,
,
∵A,B,C三点共线
∴(y+1-lnx)-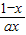 =1
=1
∴y=lnx+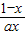 ;
;
(2)解:f(x)=lnx+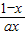 ,∴f′(x)=
,∴f′(x)=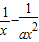
∵函数f(x)在[1,+∞)上为增函数,
∴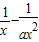 ≥0在[1,+∞)上恒成立
≥0在[1,+∞)上恒成立
∴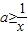
∵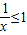 ,∴a≥1;
,∴a≥1;
(3)证明:当a=1时,f(x)=lnx+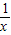 -1
-1
由(2)知,x∈[1,+∞)时,f(x)≥f(1)=0
∴lnx≥1-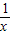 (当且仅当x=1时取“=”)
(当且仅当x=1时取“=”)
将x用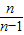 替代得ln
替代得ln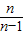 >1-
>1-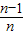 =
=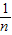
∴ln +ln
+ln +…+ln
+…+ln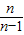 >
> +
+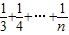
∴lnn> +
+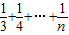
点评:本题考查向量知识的运用,考查三点共线,考查函数的单调性,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.
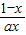 =1,从而可得结论;
=1,从而可得结论;(2)函数f(x)在[1,+∞)上为增函数,等价于f′(x)≥0在[1,+∞)上恒成立,分离参数,即可求a的范围;
(3)先证明lnx≥1-
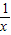 ,再将x用
,再将x用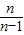 替代,即可证得结论.
替代,即可证得结论.解答:(1)解:∵
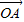 -(y+1-lnx)
-(y+1-lnx)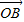 +
+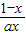
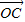 =
=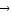 ,
,∴
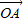 =(y+1-lnx)
=(y+1-lnx)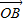 -
-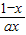
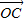 ,
,∵A,B,C三点共线
∴(y+1-lnx)-
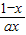 =1
=1∴y=lnx+
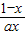 ;
;(2)解:f(x)=lnx+
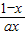 ,∴f′(x)=
,∴f′(x)=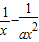
∵函数f(x)在[1,+∞)上为增函数,
∴
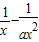 ≥0在[1,+∞)上恒成立
≥0在[1,+∞)上恒成立∴
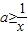
∵
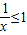 ,∴a≥1;
,∴a≥1;(3)证明:当a=1时,f(x)=lnx+
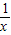 -1
-1由(2)知,x∈[1,+∞)时,f(x)≥f(1)=0
∴lnx≥1-
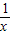 (当且仅当x=1时取“=”)
(当且仅当x=1时取“=”)将x用
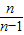 替代得ln
替代得ln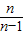 >1-
>1-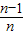 =
=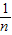
∴ln
 +ln
+ln +…+ln
+…+ln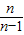 >
> +
+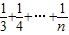
∴lnn>
 +
+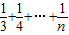
点评:本题考查向量知识的运用,考查三点共线,考查函数的单调性,考查不等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目