题目内容

定义在D上的函数f（x），如果满足：对?x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数．则下列定义在R上的函数中，不是有界函数的是

A.
f（x）=sinx²
B.
f（x）= $数学公式$
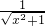
C.
f（x）=-2^1-|x|
D.
f（x）=-log₂（|x|+1）

D
分析：利用基本初等函数的性质，对A，B，C，D四个选项逐一判断即可．
解答：对于A：|f（x）|=|sinx²|≤1；
对于B：∵x²≥0，
∴x²+1≥1，于是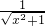 $\text{[math]}$ ≤1，
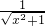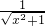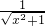∴|f（x）|= $\text{[math]}$ ≤1；
对于C：∵|x|≥0，
∴1-|x|≤1，
∴2^1-|x|≤2¹=2，
|f（x）|=|-2^1-|x||=|2^1-|x||=2^1-|x|≤2；
对于D：|f（x）|=log₂（|x|+1）≥0，
故f（x）=-log₂（|x|+1）为无界函数．
故选D．
点评：本题考查函数的值域，考查基本初等函数的性质，属于中档题．

练习册系列答案

奇迹课堂系列答案

初中伴你学习新课程系列答案

同步训练与闯关系列答案

新支点卓越课堂系列答案

优干线测试卷系列答案

优干线课课练系列答案

励耘书业初中英语专题精析系列答案

百分百全能训练系列答案

轻巧夺冠周测月考直通中考系列答案

状元成才路创优作业100分系列答案

相关题目

定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．
已知函数f（x）=1+a•（

）^x；g（x）=

（Ⅰ）当a=1时，求函数f（x）值域并说明函数f（x）在（-∞，0）上是否为有界函数？
（Ⅱ）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围；
（Ⅲ）已知m＞-1，函数g（x）在[0，1]上的上界是T（m），求T（m）的取值范围．

定义在D上的函数f（x），如果满足对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界，已知函数f（x）=1+x+ax²
（1）当a=-1时，求函数f（x）在（-∞，0）上的值域，判断函数f（x）在（-∞，0）上是否为有界函数，并说明理由；
（2）若函数f（x）在x∈[1，4]上是以3为上界的有界函数，求实数a的取值范围．

定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数f(x)=1+a•(

（1）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围；
（2）已知m＞-1，函数g（x）在[0，1]上的上界是T（m），求T（m）的取值范围．

对于定义在D上的函数f（x），若存在距离为d的两条直线y=kx+m₁和y=kx+m₂，使得对任意x∈D都有kx+m₁≤f（x）≤kx+m₂恒成立，则称函数f（x）（x∈D）有一个宽度为d的通道．给出下列函数：①f(x)=

，②f（x）=sinx，③f(x)=

，其中在区间[1，+∞）上通道宽度可以为1的函数有（　　）

如右图所示，定义在D上的函数f（x），如果满足：对?x∈D，常数A，都有f（x）≥A成立，则称函数f（x）在D上有下界，其中A称为函数的下界．（提示：图中的常数A可以是正数，也可以是负数或零）
（1）试判断函数f(x)=x3+

在（0，+∞）上是否有下界？并说明理由；
（2）已知某质点的运动方程为S(t)=at-2

，要使在t∈[0，+∞）上的每一时刻该质点的瞬时速度是以A=

为下界的函数，求实数a的取值范围．