题目内容
已知函数f(x)=ax﹣1(a>0且a≠1)
(1)若函数y=f(x)的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若f(lga)=100,求a的值.
(1)若函数y=f(x)的图象经过P(3,4)点,求a的值;
(2)比较
 大小,并写出比较过程;
大小,并写出比较过程;(3)若f(lga)=100,求a的值.
解:(1)∵函数y=f(x)的图象经过P(3,4)
∴a3﹣1=4,即a2=4.
又a>0,所以a=2.
(2)当a>1时,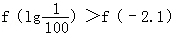 ;
;
当0<a<1时,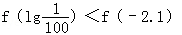 .
.
因为,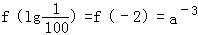 ,f(﹣2.1)=a﹣3.1
,f(﹣2.1)=a﹣3.1
当a>1时,y=ax在(﹣∞,+∞)上为增函数,
∵﹣3>﹣3.1,∴a﹣3>a﹣3.1.
即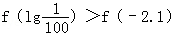 .
.
当0<a<1时,y=ax在(﹣∞,+∞)上为减函数,
∵﹣3>﹣3.1,∴a﹣3<a﹣3.1.
即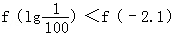 .
.
(3)由f(lga)=100知,alga﹣1=100.
所以,lgalga﹣1=2(或lga﹣1=loga100).
∴(lga﹣1)·lga=2.
∴lg2a﹣lga﹣2=0,
∴lga=﹣1或lga=2,
所以,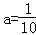 或a=100.
或a=100.
∴a3﹣1=4,即a2=4.
又a>0,所以a=2.
(2)当a>1时,
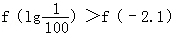 ;
;当0<a<1时,
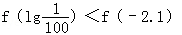 .
.因为,
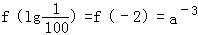 ,f(﹣2.1)=a﹣3.1
,f(﹣2.1)=a﹣3.1当a>1时,y=ax在(﹣∞,+∞)上为增函数,
∵﹣3>﹣3.1,∴a﹣3>a﹣3.1.
即
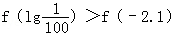 .
.当0<a<1时,y=ax在(﹣∞,+∞)上为减函数,
∵﹣3>﹣3.1,∴a﹣3<a﹣3.1.
即
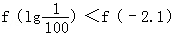 .
.(3)由f(lga)=100知,alga﹣1=100.
所以,lgalga﹣1=2(或lga﹣1=loga100).
∴(lga﹣1)·lga=2.
∴lg2a﹣lga﹣2=0,
∴lga=﹣1或lga=2,
所以,
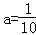 或a=100.
或a=100.
练习册系列答案
相关题目