题目内容
下列命题中假命题 是( )
A.离心率为
| ||||||
B.过点(1,1)且与直线x-2y+
| ||||||
| C.抛物线y2=2x的焦点到准线的距离为1 | ||||||
D.
|
对于A:设双曲线方程为
-
=1,则双曲线的渐近线方程为y=±
x
根据离心率为
,推断出其斜率之积为-1进而两条渐近线互相垂直,故正确;
B:设所求的直线方程为2x+y+c=0,把点(1,1)的坐标代入得 2+1+c=0,
∴c=-3,
故所求的直线的方程为2x+y-3=0,故正确;
C:根据题意可知焦点F(
,0),准线方程x=-
,
∴焦点到准线的距离是1,故正确.
D:a=3,b=5,∴c2=41,
=
,∴两准线间的距离为
=
故错.
故选 D.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
根据离心率为
| 2 |
B:设所求的直线方程为2x+y+c=0,把点(1,1)的坐标代入得 2+1+c=0,
∴c=-3,
故所求的直线的方程为2x+y-3=0,故正确;
C:根据题意可知焦点F(
| 1 |
| 2 |
| 1 |
| 2 |
∴焦点到准线的距离是1,故正确.
D:a=3,b=5,∴c2=41,
| 2a2 |
| c |
| 6 | ||
|
| 2a2 |
| c |
| 6 | ||
|
故错.
故选 D.

练习册系列答案
相关题目
 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )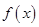 既不是奇函数,也不是偶函数 B.
既不是奇函数,也不是偶函数 B.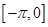 上恰有一个零点
上恰有一个零点 上是增函数
上是增函数 的双曲线的两条渐近线互相垂直
的双曲线的两条渐近线互相垂直 垂直的直线方程是2x+y-3=0
垂直的直线方程是2x+y-3=0 的两条准线之间的距离为
的两条准线之间的距离为