Question

已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的一焦点为F₁（-1，0），长轴长为2

2

，过原点的直线y=kx（k＞0）与C相交于A、B两点（B在第一象限），BH垂直x轴，垂足为H．
（1）求椭圆C的方程；
（2）当k变化时，求△ABH面积的最大值；
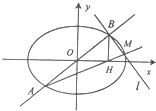
（3）过B作直线l垂直于AB，已知l与直线AH交于点M，判断点M是否在椭圆C上，证明你的结论．

Answer 1

分析：（1）利用已知可得c=1，2a=2

2

，再利用b²=a²-c²即可得到椭圆的方程；
（2）由对称性可设A（-x₀，-y₀），B（x₀，y₀），把直线AB的方程与椭圆的方程联立即可解得x₀，y₀．而S_△ABH=2S_△OBH=x₀y₀即可用k表示，再利用基本不等式即可得出．
（3）点M在椭圆上．利用直线垂直于斜率的关系可得k_AB•k_l+1=0，进而得出直线AH的斜率与l的斜率关系，再利用三点AHM共线斜率相等及点B在椭圆上满足椭圆的方程即可得出点M的坐标也满足椭圆的方程即可．

解答：解：（1）由题意可得半焦距c=1，2a=2

2

，解得a=

2

，
∴b²=a²-c²=1．
∴椭圆的方程为

x2

2

+y2=1．
（2）由对称性可设A（-x₀，-y₀），B（x₀，y₀），联立

y=kx x2+2y2=2

解得

x 2 0 = 2 1+2k2 y 2 0 = 2k2 1+2k2

，
则S_△ABH=2S_△OBH=x₀y₀=

2k

1+2k2

=

2

1 k +2k

≤

2

2 1 k •2k

=

2

2

．
当且仅当k=

2

2

时取等号，即△ABH的面积最大值为

2

2

．
（3）点M在椭圆上．下面给出证明：
设M（x₁，y₁）．由H（x₀，0）得AH的斜率k₁=

y0

2x0

=

k

2

，又BM的斜率k2=

y1-y0

x1-x0

．
∵l⊥AB，∴k₁k+1=0，即2k₁k₂+1=0，
又2k₂k₁+1=2×

y1-y0

x1-x0

•

y1-(-y0)

x1-(-x0)

+1=

( x 2 1 +2 y 2 1 )-( x 2 0 +2 y 2 0 )

x 2 1 - x 2 0

，
∴

x

2 1

+2

y

2 1

-(

x

2 0

+2

y

2 0

)=0，
∵点B（x₀，y₀）在椭圆上，∴

x

2 0

+2

y

2 0

=2，
∴

x

2 1

+2

y

2 1

=2，即

x 2 1

2

+

y

2 1

=1．
∴点M在椭圆C

x2

2

+y2=1．

点评：本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得出交点的坐标、点在椭圆上得到点的坐标适合椭圆的方程、三角形的面积计算公式、直线的斜率计算公式、基本不等式的性质等基础知识与基本技能，考查了推理能力和计算能力．