题目内容
11．已知x，y满足$\left\{\begin{array}{l}x≥1\\ x+y≤5\\ ax+by+c≤0\end{array}\right.$，记目标函数Z=2x+y的最大值为7，最小值为1，则a：b：c的值是2：（-3）：（-5）．分析 先根据约束条件画出可行域，再利用几何意义求最值，z=2x+y表示直线在y轴上的截距，只需求出可行域直线在y轴上的截距最大最小值时所在的顶点即可
解答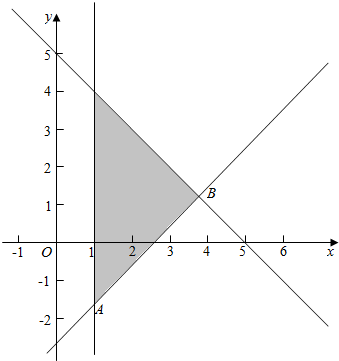 
解：由题意得：
目标函数Z=2x+y在点B取得最大值为7，
在点A处取得最小值为1，
∴A（1，-1），B（4，1），
∴直线AB的方程是：2x-3y-5=0，
所以a：b：c=2：（-3）：（-5）；
故答案为：2：（-3）：（-5）．
点评 本题主要考查了简单的线性规划，以及利用几何意义求最值的方法．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
已知函数$f（x）=Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜\frac{π}{2}）$的部分图象如图所示．
2．己知a=cos46°cos14°-sin46°sin14°，b=$\frac{1+tan35°}{1-tan35°}$，lnc=4-c2则a，b，c的大小关系为（ ）
| A． | a＜b＜c | B． | b＜c＜a | C． | a＜c＜b | D． | c＜a＜b |
在锐角△ABC中，角A、B、C所对的边分别是a、b、c，O为△ABC的外心．