Question

13．如图，已知长方体的棱AB=BC=5，AA₁=$\sqrt{5}$，则BC₁与A₁D₁所成角的正切值是$\frac{\sqrt{5}}{5}$，BC₁与B₁D₁所成角的余弦值是$\frac{\sqrt{15}}{6}$．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出BC₁与A₁D₁所成角的正切值和BC₁与B₁D₁所成角的余弦值．

解答 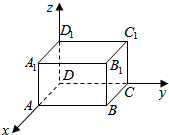解：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
∵长方体的棱AB=BC=5，AA₁=$\sqrt{5}$，
∴B（5，5，0），C₁（0，5，$\sqrt{5}$），A₁（5，0，$\sqrt{5}$），D₁（0，0，$\sqrt{5}$），${B}_{1}（5，5，\sqrt{5}）$，
$\overrightarrow{B{C}_{1}}$=（-5，0，$\sqrt{5}$），$\overrightarrow{{A}_{1}{D}_{1}}$=（-5，0，0），$\overrightarrow{{B}_{1}{D}_{1}}$=（-5，-5，0），
设BC₁与A₁D₁所成角为θ，
则cosθ=|cos＜$\overrightarrow{B{C}_{1}}，\overrightarrow{{A}_{1}{D}_{1}}$＞|=|$\frac{\overrightarrow{B{C}_{1}}•\overrightarrow{{A}_{1}{D}_{1}}}{|\overrightarrow{B{C}_{1}}|•|\overrightarrow{{A}_{1}{D}_{1}}|}$|=|$\frac{25}{\sqrt{30}•5}$|=$\frac{\sqrt{30}}{6}$，
sinθ=$\sqrt{1-（\frac{\sqrt{30}}{6}）^{2}}$=$\frac{\sqrt{6}}{6}$，∴tanθ=$\frac{\frac{\sqrt{6}}{6}}{\frac{\sqrt{30}}{6}}$=$\frac{\sqrt{5}}{5}$．
∴BC₁与A₁D₁所成角的正切值为$\frac{\sqrt{5}}{5}$．
设BC₁与B₁D₁所成角为α，
∴cosα=|cos＜$\overrightarrow{B{C}_{1}}，\overrightarrow{{B}_{1}{D}_{1}}$＞|=|$\frac{\overrightarrow{B{C}_{1}}•\overrightarrow{{B}_{1}{D}_{1}}}{|\overrightarrow{B{C}_{1}}|•|\overrightarrow{{B}_{1}{D}_{1}}|}$|=|$\frac{25}{\sqrt{30}•\sqrt{50}}$|=$\frac{\sqrt{15}}{6}$．
∴BC₁与B₁D₁所成角的余弦值是$\frac{\sqrt{15}}{6}$．
故答案为：$\frac{\sqrt{5}}{5}$，$\frac{\sqrt{15}}{6}$．

点评 本题考查异面直线所成角的正切值和余弦值的求法，是基础题，解题时要认真审题，注意向量法的合理运用．