题目内容
在△ABC中，角A，B，C的对边分别为a，b，c，且A=60°，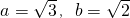
，那么角B的大小等于
- A.45°
- B.45°或135°
- C.135°
- D.60°
A
分析：由正弦定理，得sinB=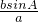
=
，所以B=45°或135°．再结合三角形内角和定理得B＜120°，得135°不符合题意，所以B=45°即为本题答案．
解答：∵△ABC中，
=
∴sinB==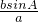
=
∵B∈（0，π），∴B=45°或135°
∵A=60°，得B+C=120°，B＜120°
∴B=45°（舍去135°）
故选：A
点评：本题给出三角形中的两边和其中一边的对角，求另一条边所对的角大小，着重考查了用正弦定理解三角形的知识，属于基础题．
分析：由正弦定理，得sinB=
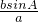=，所以B=45°或135°．再结合三角形内角和定理得B＜120°，得135°不符合题意，所以B=45°即为本题答案．解答：∵△ABC中，
=∴sinB=
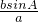==∵B∈（0，π），∴B=45°或135°
∵A=60°，得B+C=120°，B＜120°
∴B=45°（舍去135°）
故选：A
点评：本题给出三角形中的两边和其中一边的对角，求另一条边所对的角大小，着重考查了用正弦定理解三角形的知识，属于基础题．
练习册系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |