题目内容
已知数列{an}中a1=3,a2=5,其前n项和满足:Sn+Sn-2=2Sn-1+2n-1(n≥3).
(1)试求数列{an}的通项公式;
(2)令bn= ,Tn是数列{bn}的前n项和,证明:Tn<
,Tn是数列{bn}的前n项和,证明:Tn< ;
;
(3)证明:对任意的m∈(0, ),均存在n0∈N*,使得(2)中的Tn>m成立.
),均存在n0∈N*,使得(2)中的Tn>m成立.
(1)解:由Sn+Sn-2=2Sn-1+2n-1(n≥3)得Sn-Sn-1=Sn-1-Sn-2+2n-1(n≥3),
∴an=an-1+2n-1
∴an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2=2n-1+2n-2+…+22+5=2n+1(n≥3)
检验知n=1、2时,结论也成立,故an=2n+1;
(2)证明:∵bn= =
= ,
,
∴Tn=b1+b2+…+bn= [(
[( -
- )+(
)+( )+…+
)+…+ ]=
]= <
<
(3)证明:由(2)可知Tn= ,
,
若Tn>m,则得 ,化简得
,化简得 .
.
∵m∈(0, ),∴1-6m>0,∴
),∴1-6m>0,∴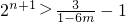 ,∴n>
,∴n> ,
,
当 <1,即0<m<
<1,即0<m< 时,取n0=1即可,
时,取n0=1即可,
当 ≥1,即
≥1,即 时,则记
时,则记 的整数部分为S,取n0=S+1即可,
的整数部分为S,取n0=S+1即可,
综上可知:对任意的m∈(0, ),均存在n0∈N*,使得(2)中的Tn>m成立.
),均存在n0∈N*,使得(2)中的Tn>m成立.
分析:(1)由Sn+Sn-2=2Sn-1+2n-1(n≥3)得an=an-1+2n-1(n≥3),利用an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2,即可求得结论;
(2)bn= =
= ,从而可求Tn,即可证得结论;
,从而可求Tn,即可证得结论;
(3)由(2)可知Tn= ,若Tn>m,则得
,若Tn>m,则得 ,化简得
,化简得 ,根据m∈(0,
,根据m∈(0, ),可得n>
),可得n> ,分类讨论,即可求得结论.
,分类讨论,即可求得结论.
点评:本题考查数列的通项与求和,考查不等式的证明,解题的关键是累加法求通项,裂项相消法求和,属于中档题.
∴an=an-1+2n-1
∴an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2=2n-1+2n-2+…+22+5=2n+1(n≥3)
检验知n=1、2时,结论也成立,故an=2n+1;
(2)证明:∵bn=
 =
= ,
,∴Tn=b1+b2+…+bn=
 [(
[( -
- )+(
)+( )+…+
)+…+ ]=
]= <
<
(3)证明:由(2)可知Tn=
 ,
,若Tn>m,则得
 ,化简得
,化简得 .
.∵m∈(0,
 ),∴1-6m>0,∴
),∴1-6m>0,∴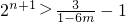 ,∴n>
,∴n> ,
,当
 <1,即0<m<
<1,即0<m< 时,取n0=1即可,
时,取n0=1即可,当
 ≥1,即
≥1,即 时,则记
时,则记 的整数部分为S,取n0=S+1即可,
的整数部分为S,取n0=S+1即可,综上可知:对任意的m∈(0,
 ),均存在n0∈N*,使得(2)中的Tn>m成立.
),均存在n0∈N*,使得(2)中的Tn>m成立.分析:(1)由Sn+Sn-2=2Sn-1+2n-1(n≥3)得an=an-1+2n-1(n≥3),利用an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+a2,即可求得结论;
(2)bn=
 =
= ,从而可求Tn,即可证得结论;
,从而可求Tn,即可证得结论;(3)由(2)可知Tn=
 ,若Tn>m,则得
,若Tn>m,则得 ,化简得
,化简得 ,根据m∈(0,
,根据m∈(0, ),可得n>
),可得n> ,分类讨论,即可求得结论.
,分类讨论,即可求得结论.点评:本题考查数列的通项与求和,考查不等式的证明,解题的关键是累加法求通项,裂项相消法求和,属于中档题.

练习册系列答案
相关题目