题目内容
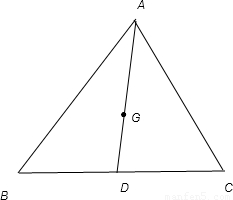
已知点G是△ABC的重心,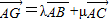 ( λ,μ∈R),若∠A=120°,
( λ,μ∈R),若∠A=120°,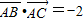 ,则
,则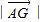 的最小值是( )
的最小值是( )A.
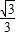
B.
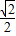
C.

D.

【答案】分析:由三角形重心的性质可得,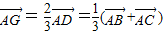 ,设
,设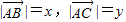 ,由向量数量积的定义可知
,由向量数量积的定义可知
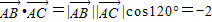 ,可得xy=4,然后根据向量数量积的性质可得|
,可得xy=4,然后根据向量数量积的性质可得|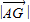 =
=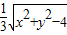 ,结合基本不等式可求
,结合基本不等式可求
解答:解:由向量加法的三角形法则及三角形重心的性质可得,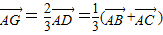
∵∠A=120°,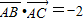 ,则根据向量的数量积的定义可得,
,则根据向量的数量积的定义可得,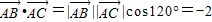
设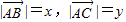
∴ 即xy=4
即xy=4
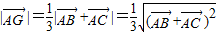 =
=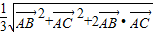 =
=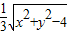
x2+y2≥2xy=8(当且仅当x=y取等号)
∴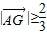 即
即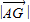 的最小值为
的最小值为
故选:C
点评:此题是一道平面向量与基本不等式结合的试题,解题的关键是利用平面向量的数量积的性质把所求的问题转化为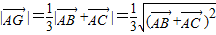 =
=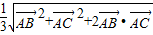 =
=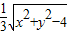 ,还利用了基本不等式求解最值.
,还利用了基本不等式求解最值.
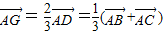 ,设
,设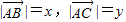 ,由向量数量积的定义可知
,由向量数量积的定义可知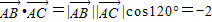 ,可得xy=4,然后根据向量数量积的性质可得|
,可得xy=4,然后根据向量数量积的性质可得|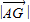 =
=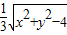 ,结合基本不等式可求
,结合基本不等式可求解答:解:由向量加法的三角形法则及三角形重心的性质可得,
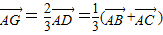
∵∠A=120°,
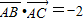 ,则根据向量的数量积的定义可得,
,则根据向量的数量积的定义可得,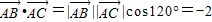
设
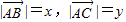
∴
 即xy=4
即xy=4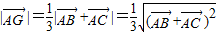 =
=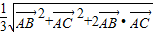 =
=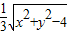
x2+y2≥2xy=8(当且仅当x=y取等号)
∴
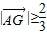 即
即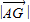 的最小值为
的最小值为
故选:C

点评:此题是一道平面向量与基本不等式结合的试题,解题的关键是利用平面向量的数量积的性质把所求的问题转化为
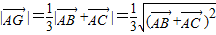 =
=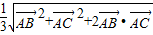 =
=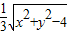 ,还利用了基本不等式求解最值.
,还利用了基本不等式求解最值. 
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知点G是△ABC的重心,点P是△GBC内一点,若
=λ
+μ
,则λ+μ的取值范围是( )
| AP |
| AB |
| AC |
A、(
| ||
B、(
| ||
C、(1,
| ||
| D、(1,2) |