Question

已知函数f（x）=|x|•（a-x），a∈R．
（1）当a=4时，画出函数f（x）的大致图象，并写出其单调递增区间；
（2）若函数f（x）在x∈[0，2]上是单调递减函数，求实数a的取值范围；
（3）若不等式|x|•（a-x）≤6对x∈[0，2]恒成立，求实数a的取值范围．

Answer 1

解：（1）a=4时，，
f（x）的图象如图所示，
所以其单调递增区间为[0，2]．
（2）x∈[0，2]时，
∴f（x）在（-∞，）上单调递增，在[，+∞）上单调递减．
又函数f（x）在x∈[0，2]上是单调递减函数，所以．
解得a≤0．
（3）当x=0时，0≤6成立，所以a∈R；
当0＜x≤2时，，
即，只要
设，则g′（x）=1-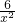，∴g（x）在上递减，在上递增，
∴当0＜x≤2时，g（x）_min=g（2）=5．
所以a≤5．
综上，|x|（a-x）≤6对x∈[0，2]恒成立的实数a的取值范围是（-∞，5]．
分析：（1）首先对x分类讨论，去掉绝对值符号；然后根据二次函数的图象特征，即可画出其草图；而其单调性，观察图象显而易见．
（2）由x∈[0，2]易于把函数f（x）化简为二次函数，再把其单调减区间表示出来，进而根据f（x）在x∈[0，2]上是单调递减函数，可得a的不等式，则a可求．
（3）要用分离参数的方法把a分离出来，需对x=0单独讨论；由于0＜x≤2时，恒成立，则利用导数法求出x+的最小值即可．
点评：二次函数的图象与性质是解决更复杂函数问题的前提，必须把此基础打牢；
分离参数法是求解不等式恒成立问题的常用思想方法，它是通过分离参数转化为不含参数的函数的最值问题求解．