题目内容
已知函数f(x)=Acos(ωx+ )(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,|
)(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,| |<
|< ,为了得到函数f(x)的图像,只要将函数g(x)=
,为了得到函数f(x)的图像,只要将函数g(x)= (x∈R)的图像上所有的点( )
(x∈R)的图像上所有的点( )

 )(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,|
)(x∈R)的图像的一部分如下图所示,其中A>0,ω>0,| |<
|< ,为了得到函数f(x)的图像,只要将函数g(x)=
,为了得到函数f(x)的图像,只要将函数g(x)= (x∈R)的图像上所有的点( )
(x∈R)的图像上所有的点( ) 
A.向右平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的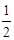 倍,纵坐标不变 倍,纵坐标不变 |
B.向右平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把得所各点的横坐标缩短到原来的 个单位长度,再把得所各点的横坐标缩短到原来的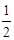 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C
分析:由 T=
T= ,可求得T,从而可求得ω,由ω?(-
,可求得T,从而可求得ω,由ω?(- )+φ=-
)+φ=-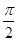 +2kπ(k∈Z)可求得φ,结合诱导公式与平移知识即可得到答案.
+2kπ(k∈Z)可求得φ,结合诱导公式与平移知识即可得到答案.
解:由f(x)=cos(ωx+φ)(x∈R)的图象可得: T=
T= -(-
-(- )=
)= π,
π,
∴T=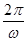 =π,
=π,
∴ω=2;又2×(- )+φ=-
)+φ=-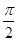 +2kπ(k∈Z),
+2kπ(k∈Z),
∴φ=2kπ+ (k∈Z),
(k∈Z),
不妨令k=0,可得φ= .
.
∴f(x)=cos(2x+ )=cos[2(x+
)=cos[2(x+ )];
)];
又g(x)=cos2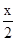 -sin2
-sin2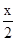 =cosx
=cosx
∴只要将函数g(x)=cosx的图象上所有的点向左平移 个单位长度,得到h(x)=cos(x+
个单位长度,得到h(x)=cos(x+ ),
),
再把h(x)=cos(x+ )各点的横坐标缩短到原来的
)各点的横坐标缩短到原来的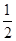 倍,纵坐标不变,即可得到f(x)=cos(2x+
倍,纵坐标不变,即可得到f(x)=cos(2x+ )的图象.
)的图象.
故选C.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,求得f(x)=cos(ωx+φ)(x∈R)中的ω,φ是关键,也是难点,属于中档题.
 T=
T= ,可求得T,从而可求得ω,由ω?(-
,可求得T,从而可求得ω,由ω?(- )+φ=-
)+φ=-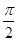 +2kπ(k∈Z)可求得φ,结合诱导公式与平移知识即可得到答案.
+2kπ(k∈Z)可求得φ,结合诱导公式与平移知识即可得到答案.解:由f(x)=cos(ωx+φ)(x∈R)的图象可得:
 T=
T= -(-
-(- )=
)= π,
π,∴T=
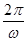 =π,
=π,∴ω=2;又2×(-
 )+φ=-
)+φ=-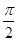 +2kπ(k∈Z),
+2kπ(k∈Z),∴φ=2kπ+
 (k∈Z),
(k∈Z),不妨令k=0,可得φ=
 .
.∴f(x)=cos(2x+
 )=cos[2(x+
)=cos[2(x+ )];
)];又g(x)=cos2
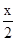 -sin2
-sin2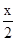 =cosx
=cosx∴只要将函数g(x)=cosx的图象上所有的点向左平移
 个单位长度,得到h(x)=cos(x+
个单位长度,得到h(x)=cos(x+ ),
),再把h(x)=cos(x+
 )各点的横坐标缩短到原来的
)各点的横坐标缩短到原来的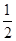 倍,纵坐标不变,即可得到f(x)=cos(2x+
倍,纵坐标不变,即可得到f(x)=cos(2x+ )的图象.
)的图象.故选C.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,求得f(x)=cos(ωx+φ)(x∈R)中的ω,φ是关键,也是难点,属于中档题.

练习册系列答案
相关题目
 ,将
,将 的图像向右平移
的图像向右平移 个单位,使得到的图像关于原点对称,则
个单位,使得到的图像关于原点对称,则 的最小值为 ( )
的最小值为 ( )



 ,则
,则 ( )
( )



 。
。 的值;
的值; 的值。
的值。
 的最小正周期与单调递减区间;
的最小正周期与单调递减区间; 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 △ABC的面积为
△ABC的面积为 ,求
,求 的值
的值




 .
. 的值是( )
的值是( )


 。
。