题目内容
设数列{a }的首项a
}的首项a =1,前n项和S
=1,前n项和S 满足关系式:3tS
满足关系式:3tS -(2t+3)S
-(2t+3)S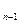 =3t(t>0,n=2,3,4…).(1)求证:数列{a
=3t(t>0,n=2,3,4…).(1)求证:数列{a }是等比数列;(2)设数列{a
}是等比数列;(2)设数列{a }的公比为f(t),若数列{b
}的公比为f(t),若数列{b }满足:b
}满足:b =1,b
=1,b =f(
=f(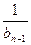 )(n=2,3,4…),求
)(n=2,3,4…),求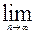
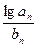 ;(3) 对于(2)中的数列{b
;(3) 对于(2)中的数列{b },求b
},求b b
b -b
-b b
b +b
+b b
b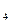 -…+(-1)
-…+(-1)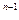 b
b b
b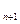 的和。
的和。
 }的首项a
}的首项a =1,前n项和S
=1,前n项和S 满足关系式:3tS
满足关系式:3tS -(2t+3)S
-(2t+3)S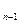 =3t(t>0,n=2,3,4…).(1)求证:数列{a
=3t(t>0,n=2,3,4…).(1)求证:数列{a }是等比数列;(2)设数列{a
}是等比数列;(2)设数列{a }的公比为f(t),若数列{b
}的公比为f(t),若数列{b }满足:b
}满足:b =1,b
=1,b =f(
=f(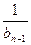 )(n=2,3,4…),求
)(n=2,3,4…),求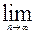
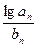 ;(3) 对于(2)中的数列{b
;(3) 对于(2)中的数列{b },求b
},求b b
b -b
-b b
b +b
+b b
b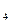 -…+(-1)
-…+(-1)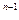 b
b b
b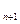 的和。
的和。(Ⅰ)见解析 (Ⅱ) 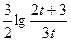
 (Ⅲ)b
(Ⅲ)b b
b -b
-b b
b +b
+b b
b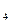 -…+(-1)
-…+(-1)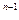 b
b b
b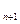 =
=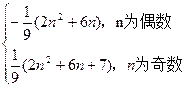
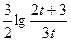
 (Ⅲ)b
(Ⅲ)b b
b -b
-b b
b +b
+b b
b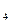 -…+(-1)
-…+(-1)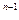 b
b b
b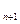 =
=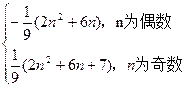
:(1)由S = a
= a =1,S
=1,S = a
= a +a
+a =1+a
=1+a ,
,
3t(1+a )-(2t+3)=3t,∴a
)-(2t+3)=3t,∴a =
=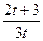 ∴
∴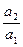 =
=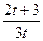
又3tS -(2t+3)S
-(2t+3)S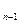 =3t,3tS
=3t,3tS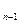 -(2t+3)S
-(2t+3)S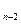 =3t两式相减
=3t两式相减
得3ta -(2t+3)a
-(2t+3)a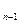 ="0" ∴
="0" ∴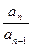 =
=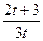 ( n=,3,4…)
( n=,3,4…)
∴{a }是首项a
}是首项a =1,公比为
=1,公比为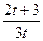 等比数列.
等比数列.
(2)∵f(t)=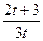 =
=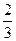 +
+ ,∴b
,∴b =f(
=f(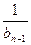 )=
)=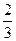 +b
+b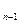
{b }是首项为1,公差为
}是首项为1,公差为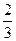 的等差数列,∴b
的等差数列,∴b =1+
=1+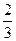 (n-1)=
(n-1)=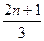
又由(1)知a =(
=(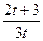 )
)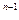 ,lga
,lga =(n-1)lg
=(n-1)lg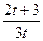
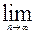
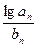 =
=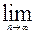
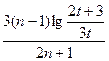 =
=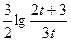

(3) 由b =
=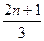 ,可知{b
,可知{b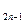 },{b
},{b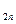 }分别是首项为1和
}分别是首项为1和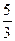 ,公差均为
,公差均为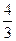 的等差数列,∴b
的等差数列,∴b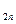 =
=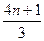 ,b
,b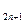 =
=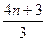 当n="2m(m=1,2,3," …)时,
当n="2m(m=1,2,3," …)时,
b b
b -b
-b b
b +b
+b b
b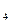 -b
-b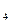 b
b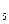 +…+b
+…+b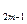 b
b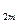 -b
-b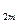 b
b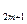
=b (b
(b -b
-b )+b
)+b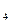 (b
(b -b
-b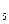 )+…+b
)+…+b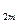 (b
(b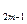 -b
-b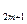 )=-
)=-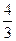 (b
(b +b
+b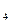 +…+b
+…+b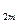 )
)
=-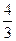
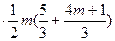 =-
=- =-
=-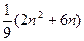
当n="2m-1(m=1,2,3," …)时,
b b
b -b
-b b
b +b
+b b
b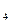 -b
-b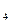 b
b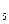 +…-b
+…-b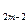 b
b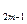 +b
+b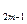 b
b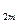
=- + b
+ b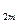 b
b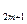 =-
=- +
+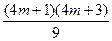
=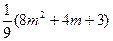 =
=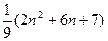
∴b b
b -b
-b b
b +b
+b b
b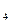 -…+(-1)
-…+(-1)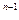 b
b b
b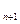 =
=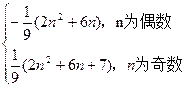
 = a
= a =1,S
=1,S = a
= a +a
+a =1+a
=1+a ,
,3t(1+a
 )-(2t+3)=3t,∴a
)-(2t+3)=3t,∴a =
=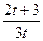 ∴
∴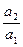 =
=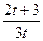
又3tS
 -(2t+3)S
-(2t+3)S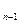 =3t,3tS
=3t,3tS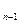 -(2t+3)S
-(2t+3)S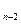 =3t两式相减
=3t两式相减得3ta
 -(2t+3)a
-(2t+3)a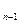 ="0" ∴
="0" ∴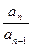 =
=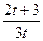 ( n=,3,4…)
( n=,3,4…)∴{a
 }是首项a
}是首项a =1,公比为
=1,公比为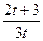 等比数列.
等比数列.(2)∵f(t)=
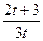 =
=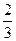 +
+ ,∴b
,∴b =f(
=f(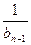 )=
)=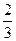 +b
+b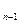
{b
 }是首项为1,公差为
}是首项为1,公差为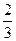 的等差数列,∴b
的等差数列,∴b =1+
=1+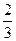 (n-1)=
(n-1)=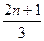
又由(1)知a
 =(
=(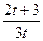 )
)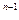 ,lga
,lga =(n-1)lg
=(n-1)lg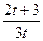
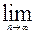
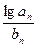 =
=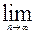
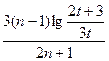 =
=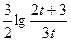

(3) 由b
 =
=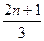 ,可知{b
,可知{b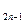 },{b
},{b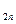 }分别是首项为1和
}分别是首项为1和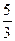 ,公差均为
,公差均为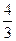 的等差数列,∴b
的等差数列,∴b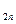 =
=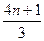 ,b
,b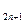 =
=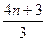 当n="2m(m=1,2,3," …)时,
当n="2m(m=1,2,3," …)时, b
 b
b -b
-b b
b +b
+b b
b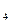 -b
-b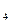 b
b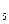 +…+b
+…+b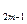 b
b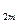 -b
-b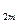 b
b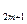
=b
 (b
(b -b
-b )+b
)+b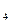 (b
(b -b
-b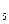 )+…+b
)+…+b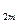 (b
(b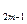 -b
-b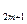 )=-
)=-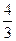 (b
(b +b
+b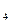 +…+b
+…+b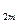 )
)=-
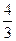
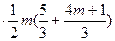 =-
=- =-
=-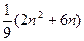
当n="2m-1(m=1,2,3," …)时,
b
 b
b -b
-b b
b +b
+b b
b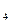 -b
-b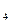 b
b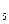 +…-b
+…-b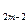 b
b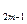 +b
+b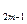 b
b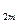
=-
 + b
+ b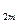 b
b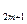 =-
=- +
+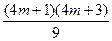
=
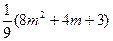 =
=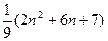
∴b
 b
b -b
-b b
b +b
+b b
b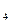 -…+(-1)
-…+(-1)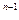 b
b b
b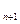 =
=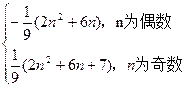

练习册系列答案
相关题目
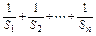 .
.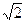 -1,a5=
-1,a5=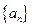 中,设
中,设 .
.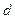 为公差的等差数列,求证
为公差的等差数列,求证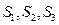 也是等差数列,并求其公差;
也是等差数列,并求其公差;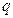 为公比的等比数列,求证
为公比的等比数列,求证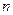 个正数
个正数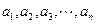 ,使这
,使这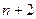 个数成等比数列;又在1与2之间插入
个数成等比数列;又在1与2之间插入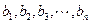 ,使这
,使这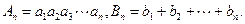 .求:
.求: 和
和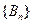 的通项;
的通项;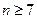 时,比较
时,比较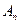 与
与 的大小,并证明你的结论
的大小,并证明你的结论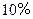 ,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)?
,那么从今年起大约几年可使总销售量达到30000台(结果保留到个位)?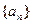 的各项均为正数,其前
的各项均为正数,其前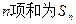 ,且
,且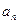 与1的等差中项等于
与1的等差中项等于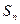 与
与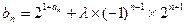 ,且数列
,且数列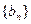 是单调递增数列。试求实数
是单调递增数列。试求实数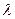 的取值范围。
的取值范围。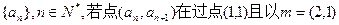 为方向向量的直线上,
为方向向量的直线上,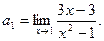 (I)求数列
(I)求数列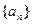 的通项公式;(II)求证:
的通项公式;(II)求证: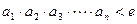 (其中e为自然对数的底数);
(其中e为自然对数的底数);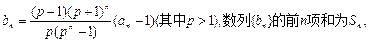
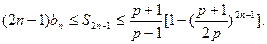
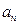 表示第
表示第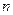 排的座位数吗?第10排能坐多少个人?
排的座位数吗?第10排能坐多少个人?