题目内容
已知空间四边形ABCD,求证:它的对角线AC和BD是异面直线.
证明:(反证法)如图2-1-12,假设AC和BD不是异面直线,则AC和BD在同一平面内.
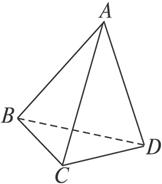
图2-1-12
∴A、B、C、D四点在同一平面内,即四边形ABCD是平面四边形,这与已知条件矛盾.
∴假设不成立.
∴AC和BD是异面直线.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
题目内容
已知空间四边形ABCD,求证:它的对角线AC和BD是异面直线.
证明:(反证法)如图2-1-12,假设AC和BD不是异面直线,则AC和BD在同一平面内.

图2-1-12
∴A、B、C、D四点在同一平面内,即四边形ABCD是平面四边形,这与已知条件矛盾.
∴假设不成立.
∴AC和BD是异面直线.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案